题目内容
9.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,右顶点、上顶点分别为A,B,直线AB被圆O:x2+y2=1截得的弦长为$\frac{2\sqrt{5}}{5}$(1)求椭圆C的方程;
(2)设过点B且斜率为k的动直线l与椭圆C的另一个交点为M,$\overrightarrow{ON}$=λ($\overrightarrow{OB}+\overrightarrow{OM}$),若点N在圆O上,求正实数λ的取值范围.
分析 (1)由题意离心率可得a=2b,设出AB所在直线方程,由圆心到直线的距离求得b,则椭圆方程可求;
(2)设点M的坐标为(x0,y0)(y0≠0),由已知向量等式得点N的坐标为(λx0,λ(y0+1)),结合N在圆上,M在椭圆上,分离参数λ求解.
解答 解:(1)由$e=\frac{\sqrt{3}}{2}$,得${e}^{2}=\frac{{c}^{2}}{{a}^{2}}=\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{3}{4}$,∴a=2b,
∴直线AB的方程为$\frac{x}{2b}+\frac{y}{b}=1$,即x+2y-2b=0,
圆心O(0,0)到直线AB的距离为d=$\sqrt{1-\frac{1}{5}}=\frac{2\sqrt{5}}{5}$,∴$\frac{2\sqrt{5}}{5}=\frac{2b}{\sqrt{5}}$,得b=1,
椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(2)设点M的坐标为(x0,y0)(y0≠0),则点N的坐标为(λx0,λ(y0+1)),
∴${λ}^{2}[{{x}_{0}}^{2}+({y}_{0}+1)^{2}]=1$,得${λ}^{2}=\frac{1}{{{x}_{0}}^{2}+{{y}_{0}}^{2}+2{y}_{0}+1}$,
又$\frac{{{x}_{0}}^{2}}{4}+{{y}_{0}}^{2}=1$,
∴${λ}^{2}=\frac{1}{-3{{y}_{0}}^{2}+2{y}_{0}+5}$,y0∈(-1,1),得${λ}^{2}≥\frac{3}{16}$,
∴正实数λ的取值范围是[$\frac{\sqrt{3}}{4},+∞$).
点评 本题考查椭圆的标准方程,考查了直线与椭圆位置关系的应用,是中档题.

| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
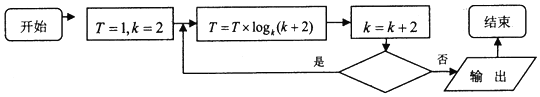
| A. | k<32 | B. | k<33 | C. | k<64 | D. | k<65 |
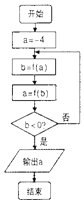
| A. | -3 | B. | $\frac{1}{16}$ | C. | $\frac{1}{4}$ | D. | 4 |
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |