题目内容
观察式子: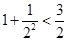 ,
,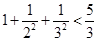 ,
,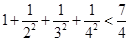 ,……则可归纳出式子(
,……则可归纳出式子(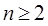 )( )
)( )
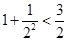 ,
,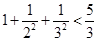 ,
,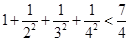 ,……则可归纳出式子(
,……则可归纳出式子(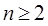 )( )
)( )A. | B. |
C. | D.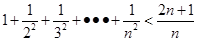 |
C
试题分析:根据题意,由每个不等式的不等号左边的最后一项的分母和右边的分母以及不等号左边的最后一
项的分母的底和指数的乘积减1等于右边分母可知,C正确;故选C.
点评:本题考查了归纳推理,培养学生分析问题的能力.

练习册系列答案
相关题目
题目内容
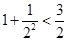 ,
,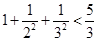 ,
,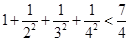 ,……则可归纳出式子(
,……则可归纳出式子(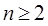 )( )
)( )A. | B. |
C. | D.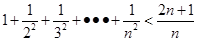 |
