题目内容
设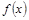 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且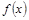 满足:“当
满足:“当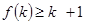 成立时,总可推出
成立时,总可推出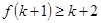 成立”,那么,下列命题总成立的是 ( )
成立”,那么,下列命题总成立的是 ( )
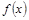 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且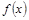 满足:“当
满足:“当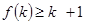 成立时,总可推出
成立时,总可推出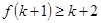 成立”,那么,下列命题总成立的是 ( )
成立”,那么,下列命题总成立的是 ( )A.若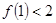 成立,则 成立,则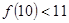 成立 成立 |
B.若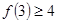 成立,则当 成立,则当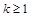 时,均有 时,均有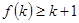 成立 成立 |
C.若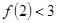 成立,则 成立,则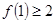 成立 成立 |
D.若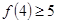 成立,则当 成立,则当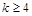 时,均有 时,均有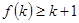 成立 成立 |
D
试题分析:“当
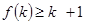 成立时,总可推出
成立时,总可推出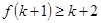 成立”是“数学归纳法”的步骤②说明如果
成立”是“数学归纳法”的步骤②说明如果 成立则
成立则 也成立这种递推关系,所以如果
也成立这种递推关系,所以如果 成立则
成立则 都成立.
都成立.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
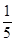 n5+
n5+ n4+
n4+ n3-
n3- n.
n.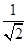 +
+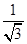 +…+
+…+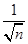 ,试比较f(n)与
,试比较f(n)与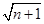 的大小.
的大小.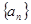 是等差数列,
是等差数列,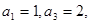 设
设 N+),
N+), N+),问Pn与Qn哪一个大?并证明你的结论.
N+),问Pn与Qn哪一个大?并证明你的结论.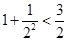 ,
,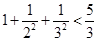 ,
,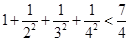 ,……则可归纳出式子(
,……则可归纳出式子(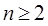 )( )
)( )


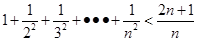
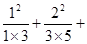 …
…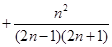 =
=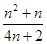
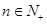 都成立.
都成立. +
+ +…+
+…+ 时,f(2k+1)-f(2k)等于 .
时,f(2k+1)-f(2k)等于 . , … … ,则可归纳出_______.
, … … ,则可归纳出_______.