题目内容
 如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,求证:
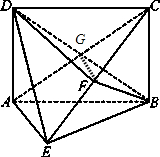
如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,求证:(1)AE∥平面BDF;
(2)平面BDF⊥平面BCE.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(1)设AC∩BD=G,连结FG,易知G是AC的中点,可证FG∥AE,从而可证AE∥平面BDF.
(2)由BC⊥平面ABE.可证BC⊥AE,由AE⊥平面BCE,可证FG⊥平面BCE,从而可证平面BDF⊥平面BCE.
(2)由BC⊥平面ABE.可证BC⊥AE,由AE⊥平面BCE,可证FG⊥平面BCE,从而可证平面BDF⊥平面BCE.
解答:
证明:(1)设AC∩BD=G,连结FG,易知G是AC的中点,
因为 F是EC中点,所以 在△ACE中,FG∥AE.…(2分)
因为 AE?平面BDF,FG?平面BDF,
所以 AE∥平面BDF. …(6分)
(2)因为 平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB,所以 BC⊥平面ABE.…(8分)
因为 AE?平面ABE,所以 BC⊥AE.…(10分)
又AE⊥BE,BC∩BE=B,所以 AE⊥平面BCE,又FG∥AE,
所以FG⊥平面BCE,…(12分)
因为 FG?平面BDF,所以平面BDF⊥平面BCE.…(14分)
因为 F是EC中点,所以 在△ACE中,FG∥AE.…(2分)
因为 AE?平面BDF,FG?平面BDF,
所以 AE∥平面BDF. …(6分)

(2)因为 平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB,所以 BC⊥平面ABE.…(8分)
因为 AE?平面ABE,所以 BC⊥AE.…(10分)
又AE⊥BE,BC∩BE=B,所以 AE⊥平面BCE,又FG∥AE,
所以FG⊥平面BCE,…(12分)
因为 FG?平面BDF,所以平面BDF⊥平面BCE.…(14分)
点评:本题主要考察了平面与平面垂直的判定,直线与平面平行的判定,连接GF,证明FG∥AE是解题的关键,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
在平行四边形ABCD中,M,N是线段BC,CD的中点,若
=m
+n
,则m+n=( )
| AC |
| BN |
| DM |
| A、2 | B、3 | C、4 | D、5 |
已知P={x|2kπ≤x≤(2k+1)π,k∈z},Q={x|-4≤x≤4},则P∩Q=( )
| A、∅ |
| B、{x|-4≤x≤-π或0≤x≤π} |
| C、{x|-4≤x≤4} |
| D、{x|0≤x≤π} |
已知实数x,y满足
则z=2x-y的最小值是( )
|
| A、5 | ||
B、
| ||
| C、-5 | ||
D、-
|
 直三棱柱ABC-A1B1C1中,CB1⊥BA1,∠CAB=
直三棱柱ABC-A1B1C1中,CB1⊥BA1,∠CAB=