题目内容
已知命题p：lg（x2-2x-2）≥0，命题q：x2＜16且x＞0，若p∧q为假，p∨q为真，求实数x的取值范围．
考点：复合命题的真假
专题：简易逻辑
分析：通过解不等式分别求出p，q，￢p，￢q的x的范围，通过讨论p真q假，p假q真，从而得到答案．
解答：
解：由x2-2x-2≥1，解得：x≥3或x≤-1，
∴p：x≥3或x≤-1，￢p：-1＜x＜3，
而q：0＜x＜4，￢q：x≤0或x≥4，
若p∧q为假，p∨q为真，则p，q一真一假，
p真q假时：
，解得：x≥4或x≤-1，
p假q真时：
，解得：0＜x＜3，
综上：x∈{x|0＜x＜3或x≤-1或x≥4}．
∴p：x≥3或x≤-1，￢p：-1＜x＜3，
而q：0＜x＜4，￢q：x≤0或x≥4，
若p∧q为假，p∨q为真，则p，q一真一假，
p真q假时：
|
p假q真时：
|
综上：x∈{x|0＜x＜3或x≤-1或x≥4}．
点评：本题考查了复合命题真假的判断，本题属于基础题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知α是第三象限的角，那么
是（ ）象限的角．
| α |
| 2 |
| A、第二 | B、第三 |
| C、第二或第三 | D、第二或第四 |
已知α是第四象限的角，若cosα=
，则tanα=（ ）
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
幂函数f（x）的图象过点（3，
），则f（x）的解析式为（ ）
| 3 |
| A、f（x）=3x | ||
| B、f（x）=x3 | ||
C、f（x）=x
| ||
D、f（x）=（
|
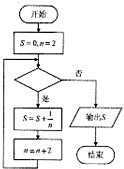阅读如图所示的程序框图，运行相应的程序，若输出的S为| 11 |
| 12 |
| A、n=6 | B、n＜6 |
| C、n≤6 | D、n≤8 |