题目内容
设斜率为2的直线l过抛物线y2=ax(a≠0)的焦点F,且和y轴交于点A.若△OAF(O为坐标原点)的面积为4,则抛物线方程为( )
A.y2=±4x B.y2=±8x
C.y2=4x D.y2=8x
B
[解析] 本小题考查抛物线的有关概念以及直线与抛物线关系.
由已知得抛物线焦点为F ,
,
 ∴a2=64,∴a=±8,∴抛物线的方程为y2=±8x.
∴a2=64,∴a=±8,∴抛物线的方程为y2=±8x.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程为 =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;
③线性相关系数r和相关指数R2都是描述线性相关强度的量,r和R2越大,相关强度越强.
④在一个2×2列联表中,计算得χ2=13.079,则有99%的把握确认这两个变量间有关系.
其中错误的个数是( )
A.0 B.1
C.2 D.3
本题可以参考独立性检验临界值表:
| P(χ2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 |
| P(χ2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 D.14+6
D.14+6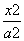 +
+ =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为( )
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A、B两点.若AB的中点坐标为(1,-1),则E的方程为( )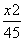 +
+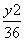 =1 B.
=1 B.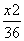 +
+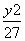 =1
=1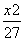 +
+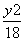 =1 D.
=1 D.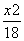 +
+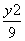 =1
=1 ,则cos
,则cos 的值为( )
的值为( )
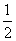
 D.
D.
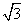 ,BC=4.
,BC=4. ,若DE∥平面PAB,求λ的值.
,若DE∥平面PAB,求λ的值.
