题目内容
在极坐标系中, 为极点,点
为极点,点 (2,
(2, ),
), (
( ).
).
(Ⅰ)求经过 ,
, ,
, 的圆
的圆 的极坐标方程;
的极坐标方程;
(Ⅱ)以极点为坐标原点,极轴为 轴的正半轴建立平面直角坐标系,圆
轴的正半轴建立平面直角坐标系,圆 的参数方程为
的参数方程为 是参数,
是参数, 为半径),若圆
为半径),若圆 与圆
与圆 相切,求半径
相切,求半径 的值.
的值.
(Ⅰ) (Ⅱ)
(Ⅱ) 或
或
解析试题分析:(Ⅰ)先以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,再将O、A、B三点的极坐标化为直角坐标,利用待定系数法设出圆的标准方程或一般方程,将O、A、B的坐标代入方程,列出关于参数的方程组,解出参数,就求出了过OAB三点的圆的方程,再利用直角坐标方程与极坐标方程的互化公式,将过OAB三点圆的直角坐标方程化为极坐标方程;(Ⅱ)将圆D的参数方程化为普通方程,求出圆心坐标与半径,由(Ⅰ)中圆C的直角坐标方程求出圆心C的坐标与半径,利用两圆相切,圆心间的距离等于半径之和或之差,列出关于 的方程,解出
的方程,解出 .
.
试题解析:(Ⅰ)以极点为坐标原点,极轴为x轴的正半轴建立平面直角坐标系,
∴点O(0,0),A(0,2),B(2,2);
过O,A,B三点的圆C的普通方程是(x-1)2+(y-1)2=2,
即x2-2x+y2-2y=0;
化为极坐标方程是ρ2=2ρcosθ+2ρsinθ,
即 5分
5分
( II)圆D的参数方程 是参数,
是参数, 为半径)化为普通方程是(x+1)2+(y+1)2=a2;
为半径)化为普通方程是(x+1)2+(y+1)2=a2;
圆C与圆D的圆心距|CD|= =
= ,
,
当圆C与圆D相切时, =
= 或
或 =
= ,解得
,解得 或
或 . 10分
. 10分
考点:极坐标与做极坐标互化,待定系数法,圆的标准方程,直角坐标方程与极坐标方程互化,参数方程与普通方程互化,两圆的位置关系

练习册系列答案
相关题目
 所表示曲线的直角坐标方程是 .
所表示曲线的直角坐标方程是 . 化为直角坐标方程是________________
化为直角坐标方程是________________  轴正半轴,直线
轴正半轴,直线 的参数方程为
的参数方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为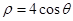 .
. 、
、 两点,求
两点,求 .
. 的方程为
的方程为 (
( 为参数),曲线
为参数),曲线 的极坐标方程为
的极坐标方程为 ,若曲线
,若曲线 的值;
的值; 到
到 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C. 与C的交点为
与C的交点为 ,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段 的中点且与
的中点且与 垂直的直线的极坐标方程.
垂直的直线的极坐标方程. sinθ)=2的距离为d.求d的最大值.
sinθ)=2的距离为d.求d的最大值.