题目内容
将圆 上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(1)写出C的参数方程;
(2)设直线 与C的交点为
与C的交点为 ,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段
,以坐标原点为极点,x轴正半轴为极坐标建立极坐标系,求过线段 的中点且与
的中点且与 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
(1) (
( 为参数);(2)
为参数);(2)
解析试题分析:(1)由平面直角坐标系中的伸缩变换得变换前后对应的坐标关系.即 ,反解
,反解 并代入圆
并代入圆 中,得曲线C的普通方程.进而写出 参数方程;(2)将直线
中,得曲线C的普通方程.进而写出 参数方程;(2)将直线 与圆
与圆 联立,求的交点
联立,求的交点 的坐标,从而可确定与
的坐标,从而可确定与 垂直的直线方程
垂直的直线方程 .再利用
.再利用 化直线的直角坐标方程为极坐标方程.
化直线的直角坐标方程为极坐标方程.
(1)设 为圆上的点,经变换为
为圆上的点,经变换为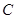 上点
上点 .依题意,得
.依题意,得 由
由 得
得 .
.
即曲线 的方程为
的方程为 .故C的参数方程为
.故C的参数方程为 (
( 为参数).
为参数).
(2)由 解得
解得 或
或 不妨设
不妨设 .则线段
.则线段 的中点坐标为
的中点坐标为 .
.
所求直线的斜率为 .于是所求直线方程为
.于是所求直线方程为 .化为极坐标方程为
.化为极坐标方程为
 ,即
,即 .
.
考点:1、伸缩变换;2、曲线的参数方程;2、曲线的极坐标方程.

练习册系列答案
相关题目
 为极点,点
为极点,点 (2,
(2, ),
), (
( ).
). 的极坐标方程;
的极坐标方程; 轴的正半轴建立平面直角坐标系,圆
轴的正半轴建立平面直角坐标系,圆 的参数方程为
的参数方程为 是参数,
是参数, 为半径),若圆
为半径),若圆
 ,直线
,直线 方程为
方程为 (t为参数),直线
(t为参数),直线 ,
, ,圆M的参数方程为
,圆M的参数方程为 。求:(1)将直线的极坐标方程化为直角坐标方程;
。求:(1)将直线的极坐标方程化为直角坐标方程;  的极坐标方程是
的极坐标方程是 ,以极点为原点,极轴为
,以极点为原点,极轴为 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
 作倾斜角为
作倾斜角为 的直线
的直线 与曲线
与曲线 两点,求线段
两点,求线段 的长度和
的长度和 的值.
的值. 的极坐标方程为
的极坐标方程为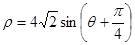 ,现以极点
,现以极点 为原点,极轴为
为原点,极轴为 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线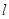 的参数方程为
的参数方程为 (
(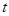 为参数)
为参数) 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆 的极坐标方程为
的极坐标方程为 .
.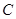 的直角坐标方程;
的直角坐标方程; 是直线
是直线 ≤
≤ 的公共点,求
的公共点,求 的取值范围.
的取值范围. 上的动点
上的动点 与定点
与定点 的最近距离是 .
的最近距离是 . (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为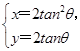 (θ为参数),试求直线l与曲线C的普通方程,并求出它们的公共点的坐标.
(θ为参数),试求直线l与曲线C的普通方程,并求出它们的公共点的坐标.