题目内容
已知直线的参数方程为为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,圆的极坐标方程为.求:(1)求圆的直角坐标方程;
(2)若是直线与圆面≤的公共点,求的取值范围.
(1);(2)[-2,2]
解析试题分析:(1)因为圆的极坐标方程为所以
所以,所以圆的直角坐标方程为:;(2) 『解法1』:
设,由圆的方程,所以圆的圆心是,半径是,将代入得,又直线过,圆的半径是,由参数t的几何意义有:,所以『解法2』:直线的参数方程化成普通方程为:,由解得,,因为是直线与圆面的公共点,所以点在线段上,所以的最大值是,最小值是,因此的取值范围是
试题解析:(1)因为圆的极坐标方程为
所以
又
所以
所以圆的直角坐标方程为:.
(2)『解法1』:
设
由圆的方程
所以圆的圆心是,半径是
将代入得
又直线过,圆的半径是,由题意有:
所以
即的取值范围是.
『解法2』:
直线的参数方程化成普通方程为:
由
解得,
∵是直线与圆面的公共点,
∴点在线段上,
∴的最大值是,
最小值是
∴的取值范围是.
考点:1.极坐标与直角坐标的互化;2.参数方程与普通方程的互化;3.线性规化的最优解

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的图象恰好通过
的图象恰好通过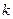 个格点,则称函数
个格点,则称函数 ; ②
; ②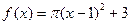 ;
; ; ④
; ④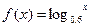 .其中是一阶格点函数的有 (填上所有满足题意的序号)
.其中是一阶格点函数的有 (填上所有满足题意的序号) 为极点,点
为极点,点 (2,
(2, ),
), (
( ).
). 的极坐标方程;
的极坐标方程; 轴的正半轴建立平面直角坐标系,圆
轴的正半轴建立平面直角坐标系,圆 的参数方程为
的参数方程为 是参数,
是参数, 为半径),若圆
为半径),若圆 ,求:
,求: 中
中 的最大值和最小值.
的最大值和最小值. ,圆M的参数方程为
,圆M的参数方程为 。求:(1)将直线的极坐标方程化为直角坐标方程;
。求:(1)将直线的极坐标方程化为直角坐标方程;  化为对应的直角坐标方程是 。
化为对应的直角坐标方程是 。 ,
, )为圆心,
)为圆心,