题目内容
7. 已知四棱锥P-ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底面 ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底面 ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.(1)证明:DN∥平面PMB;
(2)证明:平面PMB⊥平面PAD;
(3)直线PB与平面PCD所成角的正弦值.
分析 (1)取PB中点Q,连结MQ、NQ,利用三角形中位线定理和菱形的性质,证出DN∥MQ.利用线面平行判定定理,即可证出DN∥平面PMB;
(2)由菱形ABCD中∠A=60°,得到△ABD是正三角形,从而MB⊥AD.由PD⊥底ABCD得到PD⊥MB,利用线面垂直的判定定理,证出MB⊥平面PAD,结合面面垂直判定定理可得平面PMB⊥平面PAD;
(3)证明△BCD为等边三角形,设CD中点为E,连接PE,DE,可得∠PBE为直线PB与平面PCD所成角.
解答  (1)证明:取PB中点Q,连结MQ、NQ,
(1)证明:取PB中点Q,连结MQ、NQ,
因为M、N分别是棱AD、PC中点,
所以QN∥BC∥MD,且QN=MD,于是DN∥MQ.
∵MQ?平面PMB,DN?平面PMB
∴DN∥平面PMB;…(5分)
(2)证明:∵PD⊥底ABCD,MB?平面ABCD,
∴PD⊥MB
又∵底面ABCD为菱形,∠A=60°且M为AD中点,
∴MB⊥AD.
又∵AD、PD是平面PAD内的相交直线,∴MB⊥平面PAD.
∵MB?平面PMB,∴平面PMB⊥平面PAD; …(8分)
(3)解:设CD中点为E,连接PE,DE,
∵底面ABCD是∠A=60°、边长为a 的菱形
∴△BCD是等边三角形,
∴BE⊥DC,
∵PD⊥底面 ABCD,
∴PD⊥BE,
∴BE⊥平面PCD,
∴∠PBE为直线PB与平面PCD所成角,
∵BE=$\frac{\sqrt{3}}{2}$a,PA=$\sqrt{2}a$,
∴sin∠BPE=$\frac{\sqrt{6}}{4}$…(12分)
点评 本题给出特殊的四棱锥,求证线面平行、面面垂直并求直线与平面所成的角,着重考查了空间平行、垂直位置关系的判断与证明和空间角的求法等知识,属于中档题.

练习册系列答案
相关题目
16.已知函数$f(x)=cosx+{2^x}-\frac{1}{2}(x<0)$与g(x)=cosx+log2(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
| A. | $(-∞,-\sqrt{2})$ | B. | $(-∞,-\frac{{\sqrt{2}}}{2})$ | C. | $(-\sqrt{2},\frac{{\sqrt{2}}}{2})$ | D. | $(-∞,\sqrt{2})$ |
17.已知抛物线x2=2px(p>0)经过点线$M({\frac{1}{2},2})$,则它的准线方程为( )
| A. | $y=-\frac{1}{32}$ | B. | B | C. | C | D. | D |
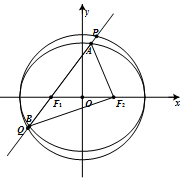 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=a2,F1(-1,0),F2(1,0)分别是椭圆的左、右两焦点,过F1且倾斜角为α$({α∈({0,\frac{π}{2}}]})$的动直线l交椭圆C于A,B两点,交圆O于P,Q两点(如图所示,点A在x轴上方).当α=$\frac{π}{4}$时,弦PQ的长为$\sqrt{14}$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)和圆O:x2+y2=a2,F1(-1,0),F2(1,0)分别是椭圆的左、右两焦点,过F1且倾斜角为α$({α∈({0,\frac{π}{2}}]})$的动直线l交椭圆C于A,B两点,交圆O于P,Q两点(如图所示,点A在x轴上方).当α=$\frac{π}{4}$时,弦PQ的长为$\sqrt{14}$. 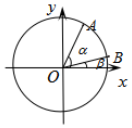 如图,在平面直角坐标系xOy中,以x轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知$A(\frac{{\sqrt{5}}}{5},\;\frac{{2\sqrt{5}}}{5})\;,\;\;B(\frac{{7\sqrt{2}}}{10},\;\frac{{\sqrt{2}}}{10})$
如图,在平面直角坐标系xOy中,以x轴为始边作两个锐角α,β,它们的终边分别与单位圆交于A,B两点.已知$A(\frac{{\sqrt{5}}}{5},\;\frac{{2\sqrt{5}}}{5})\;,\;\;B(\frac{{7\sqrt{2}}}{10},\;\frac{{\sqrt{2}}}{10})$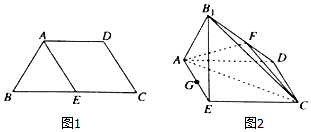 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使平面B1AE⊥平面ABCD,F,G分别为B1D,AE的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使平面B1AE⊥平面ABCD,F,G分别为B1D,AE的中点.