题目内容
 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.(Ⅰ)求AD边所在直线的方程;
(Ⅱ)求矩形ABCD的面积.
分析:(Ⅰ)由已知求出AD边所在直线的斜率,再由点T(-1,1)在AD边所在直线上,利用直线方程的点斜式求直线方程;
(Ⅱ)分别求出M到直线AB和AD的距离,然后直接由矩形面积公式得答案.
(Ⅱ)分别求出M到直线AB和AD的距离,然后直接由矩形面积公式得答案.
解答:解:(I)∵AB边所在直线的方程为x-3y-6=0,且AD与AB垂直,
∴直线AD的斜率为-3.又因为点T(-1,1)在直线AD上,
∴AD边所在直线的方程为y-1=-3(x+1),即3x+y+2=0;
(2)点M到AB边的距离是d1=
=
=
,
点M到AD边的距离是d2=
=
=
,
∴矩形ABCD的面积S=2×
×2×
=
.
∴直线AD的斜率为-3.又因为点T(-1,1)在直线AD上,
∴AD边所在直线的方程为y-1=-3(x+1),即3x+y+2=0;
(2)点M到AB边的距离是d1=
| |2-6| | ||
|
| 4 | ||
|
2
| ||
| 5 |
点M到AD边的距离是d2=
| |3×2+2| | ||
|
| 8 | ||
|
4
| ||
| 5 |
∴矩形ABCD的面积S=2×
2
| ||
| 5 |
4
| ||
| 5 |
| 64 |
| 5 |
点评:本题考查了两直线垂直与斜率的关系,考查了点到直线的距离公式,训练了矩形面积的求法,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
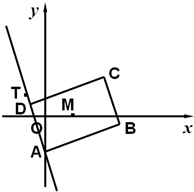 如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.求:
如图,矩形ABCD的两条对角线相交于点M(2,0),AB边所在直线的方程为x-3y-6=0,点T(-1,1)在AD边所在直线上.求: (2012•江苏一模)如图,矩形ABCD的三个顶点A、B、C分别在函数
(2012•江苏一模)如图,矩形ABCD的三个顶点A、B、C分别在函数 如图,矩形ABCD的对角线AC,BD交于O,AB=4,AD=3.沿AC把△ACD折起,使二面角D1-AC-B为直二面角.
如图,矩形ABCD的对角线AC,BD交于O,AB=4,AD=3.沿AC把△ACD折起,使二面角D1-AC-B为直二面角.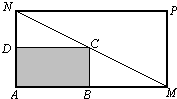 (2008•佛山二模)某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米.
(2008•佛山二模)某物流公司购买了一块长AM=30米、宽AN=20米的矩形地块,规划建设占地如图中矩形ABCD的仓库,其余地方为道路或停车场,要求顶点C在地块对角线MN上,顶点B,D分别在边AM,AN上,设AB长度为x米. 如图,矩形ABCD的边长分别为2和1,阴影部分是直线y=1和抛物线y=x2围成的部分,在矩形ABCD中随机撒100粒豆子,落到阴影部分70粒,据此可以估计出阴影部分的面积是
如图,矩形ABCD的边长分别为2和1,阴影部分是直线y=1和抛物线y=x2围成的部分,在矩形ABCD中随机撒100粒豆子,落到阴影部分70粒,据此可以估计出阴影部分的面积是