题目内容
3.已知偶函数f(x)在[0,+∞)上单调递减,若f(2x-1)>f($\frac{5}{3}$)成立,则x的取值范围是-$\frac{1}{3}$<x<$\frac{4}{3}$.分析 根据函数奇偶性和单调性的关系将不等式进行转化求解即可.
解答 解:∵偶函数f(x)在[0,+∞)上单调递减,若f(2x-1)>f($\frac{5}{3}$)成立,
∴不等式等价为f(|2x-1|)>f($\frac{5}{3}$),
即|2x-1|<$\frac{5}{3}$,
即-$\frac{5}{3}$<2x-1<$\frac{5}{3}$,
得-$\frac{1}{3}$<x<$\frac{4}{3}$,
即x的取值范围是-$\frac{1}{3}$<x<$\frac{4}{3}$,
故答案为:-$\frac{1}{3}$<x<$\frac{4}{3}$.
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性的关系将不等式进行转化是解决本题的关键.

练习册系列答案
相关题目
14.y=$\root{3}{{x}^{2}}$的导数是( )
| A. | 3x2 | B. | $\frac{1}{3}$x2 | C. | -$\frac{2}{3}$x${\;}^{-\frac{1}{3}}$ | D. | $\frac{2}{3}$x${\;}^{-\frac{1}{3}}$ |

 C.
C. D.
D.
 为等比数列,且
为等比数列,且 成等比数列,则
成等比数列,则 的值为____________.
的值为____________.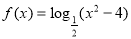 的单调减区间是
的单调减区间是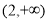 ;
;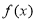 满足
满足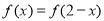 ,则
,则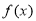 图象关于直线
图象关于直线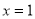 对称;
对称;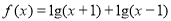 是偶函数;
是偶函数;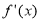 是函数
是函数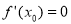 ,则
,则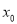 是
是