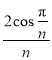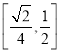题目内容
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)求曲线![]() 的直角坐标方程与直线l的参数方程;
的直角坐标方程与直线l的参数方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
【答案】(1)![]() ,
,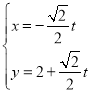 (
(![]() 为参数);(2)
为参数);(2)![]() .
.
【解析】
(1)将曲线![]() 的极坐标方程两边同乘
的极坐标方程两边同乘![]() ,根据公式即可化简为直角坐标方程;根据已知信息,直接写出直线的参数方程,整理化简即可;
,根据公式即可化简为直角坐标方程;根据已知信息,直接写出直线的参数方程,整理化简即可;
(2)联立曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的参数方程,得到关于
的参数方程,得到关于![]() 的一元二次方程,根据直线参数方程中参数的几何意义,求得结果.
的一元二次方程,根据直线参数方程中参数的几何意义,求得结果.
(1)因为![]() ,所以
,所以![]() ,
,
所以![]() ,即曲线
,即曲线![]() 的直角坐标方程为:
的直角坐标方程为:![]() ,
,
直线![]() 的参数方程
的参数方程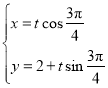 (
(![]() 为参数),
为参数),
即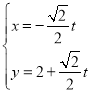 (
(![]() 为参数).
为参数).
(2)设点![]() ,
,![]() 对应的参数分别为
对应的参数分别为![]() ,
,![]() ,
,
将直线![]() 的参数方程代入曲线
的参数方程代入曲线![]() 的直角坐标方程,
的直角坐标方程,
得![]() ,
,
整理,得![]() ,
,
所以 ,
,
因为![]()
所以![]()
![]() =
=![]() ,
,
![]()
![]() =4,
=4,
所以![]() =
=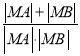
![]() .
.

【题目】近几年,电商行业的蓬勃发展带动了快递业的迅速增长,快递公司揽收价格一般是采用“首重+续重”的计价方式.首重是指最低的计费重量,续重是指超过首重部分的计费重量,不满一公斤按一公斤计费.某快递网点将快件的揽收价格定为首重(不超过一公斤)8元,续重2元/公斤(例如,若一个快件的重量是0.6公斤,按8元计费;若一个快件的重量是1.4公斤,按![]() 元
元![]() 元
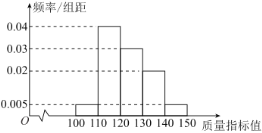
元![]() 元计费).根据历史数据,得到该网点揽收快件重量的频率分布直方图如下图所示
元计费).根据历史数据,得到该网点揽收快件重量的频率分布直方图如下图所示
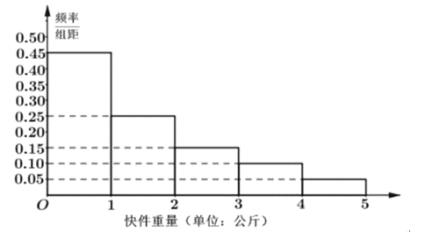
(1)根据样本估计总体的思想,将频率视作概率,求该网点揽收快件的平均价格;
(2)为了获得更大的利润,该网点对“一天中收发一件快递的平均成本![]() (单位:元)与当天揽收的快递件数
(单位:元)与当天揽收的快递件数![]() (单位:百件)
(单位:百件)![]() 之间的关系”进行调查研究,得到相关数据如下表:
之间的关系”进行调查研究,得到相关数据如下表:
每天揽收快递件数 | 2 | 3 | 4 | 5 | 8 |
每件快递的平均成本 | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 |
根据以上数据,技术人员分别根据甲、乙两种不同的回归模型,得到两个回归方程:
方程甲:![]() ,方程乙:
,方程乙:![]() .
.
①为了评价两种模型的拟合效果,根据上表数据和相应回归方程,将以下表格填写完整(结果保留一位小数),分别计算模型甲与模型乙的残差平方和![]() ,
,![]() ,并依此判断哪个模型的拟合效果更好(备注:
,并依此判断哪个模型的拟合效果更好(备注:![]() 称为相应于点
称为相应于点![]() 的残差,残差平方和
的残差,残差平方和![]() ;
;
每天揽收快递件数 | 2 | 3 | 4 | 5 | 8 | |
每天快递的平均成本 | 5.6 | 4.8 | 4.4 | 4.3 | 4.1 | |
模型甲 | 预报值 | 5.2 | 5.0 | 4.8 | ||
残差 |
| 0.2 | 0.4 | |||
模型乙 | 预报值 | 5.5 | 4.8 | 4.5 | ||
预报值 |
| 0 | 0.1 | |||
②预计该网点今年6月25日(端午节)一天可以揽收1000件快递,试根据①中确定的拟合效果较好的回归模型估计该网点当天的总利润(总利润=(平均价格-平均成本)×总件数).