题目内容
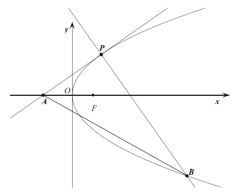
【题目】设![]() ,
,![]() 是抛物线
是抛物线![]() 上的两个不同的点,
上的两个不同的点,![]() 是坐标原点.若直线
是坐标原点.若直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,则( ).
,则( ).
A.![]() B.以
B.以![]() 为直径的圆的面积大于
为直径的圆的面积大于![]()
C.直线![]() 过定点
过定点![]() D.点
D.点![]() 到直线
到直线![]() 的距离不大于2
的距离不大于2
【答案】CD
【解析】
通过![]() 轴时的特殊情况,判断A、B选项不正确;当直线
轴时的特殊情况,判断A、B选项不正确;当直线![]() 与
与![]() 轴不垂直时,设
轴不垂直时,设![]() 直线方程,通过推理论证,得出直线过定点
直线方程,通过推理论证,得出直线过定点![]() ,进而得出点
,进而得出点![]() 到直线
到直线![]() 的距离最大值即为O、Q两点间的距离,进而得出CD正确.
的距离最大值即为O、Q两点间的距离,进而得出CD正确.
不妨设![]() 为第一象限内的点,
为第一象限内的点,
①当直线![]() 轴时,
轴时,![]() ,由
,由![]() ,
,
得![]() ,
,![]() ,
,
所以直线![]() ,
,![]() 的方程分别为:
的方程分别为:![]() 和
和![]() .
.
与抛物线方程联立,得![]() ,
,![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,此时
,此时![]() ,
,
以![]() 为直径的圆的面积
为直径的圆的面积![]() ,故A、B不正确.
,故A、B不正确.
②当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() ,
,
与抛物线方程联立消去![]() ,得
,得![]() ,则
,则![]() .
.
设![]() ,
,![]() ,则
,则![]() .
.
因为![]() ,所以
,所以![]() ,
,
则![]() ,则
,则![]() ,
,
所以![]() ,即
,即![]() ,
,
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
综上可知,直线![]() 为恒过定点
为恒过定点![]() 的动直线,故C正确;
的动直线,故C正确;
易知当![]() 时,原点
时,原点![]() 到直线
到直线![]() 的距离最大,最大距离为2,
的距离最大,最大距离为2,
即原点![]() 到直线
到直线![]() 的距离不大于2.故D正确.
的距离不大于2.故D正确.
故选:CD

练习册系列答案
相关题目