题目内容
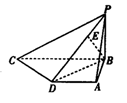
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1

(1)证明:AB=AC
(2)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小

(1)证明:AB=AC
(2)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小
(1)详见解析,(2)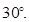
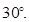
试题分析:(1)证明AB=AC,往往转化为证明对应线段垂直,即证
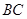 边上中线垂直
边上中线垂直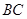 .取BC中点F,连接EF,AF,易得ADEF为平行四边形,从而AF//DE. 又DE⊥平面
.取BC中点F,连接EF,AF,易得ADEF为平行四边形,从而AF//DE. 又DE⊥平面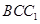 ,可得AF⊥BC.(2)求直线与平面所成角的关键在于找面的垂线.而面的垂线,往往从面面垂直的性质定理中取到.观察图形可知,BC⊥平面DEF,从而平面BCD⊥平面DEF.过
,可得AF⊥BC.(2)求直线与平面所成角的关键在于找面的垂线.而面的垂线,往往从面面垂直的性质定理中取到.观察图形可知,BC⊥平面DEF,从而平面BCD⊥平面DEF.过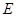 作两平面的交线
作两平面的交线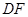 的垂线就是平面BCD的垂线.因为本题三维垂直关系已知,所以也可利用空间向量进行求解.已知条件的二面角与所求线面角有一个相同的平面,这也简化了运算量.
的垂线就是平面BCD的垂线.因为本题三维垂直关系已知,所以也可利用空间向量进行求解.已知条件的二面角与所求线面角有一个相同的平面,这也简化了运算量.试题解析:
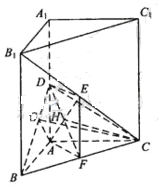
解法一:(1)取BC中点F,连接EF,则EF
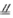
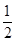
 ,从而EF
,从而EF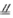 DA。
DA。连接AF,则ADEF为平行四边形,从而AF//DE。又DE⊥平面
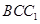 ,故AF⊥平面
,故AF⊥平面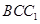 ,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC。 5分
,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC。 5分(2)作AG⊥BD,垂足为G,连接CG。由三垂线定理知CG⊥BD,故∠AGC为二面角A-BD-C的平面角。由题设知,∠AGC=600..
设AC=2,则AG=
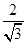 。又AB=2,BC=
。又AB=2,BC=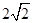 ,故AF=
,故AF=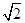 。
。由
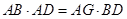 得2AD=
得2AD=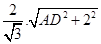 ,解得AD=
,解得AD=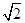 。 9分
。 9分故AD=AF。又AD⊥AF,所以四边形ADEF为正方形。
因为BC⊥AF,BC⊥AD,AF∩AD=A,故BC⊥平面DEF,因此平面BCD⊥平面DEF。
连接AE、DF,设AE∩DF=H,则EH⊥DF,EH⊥平面BCD。
连接CH,则∠ECH为
 与平面BCD所成的角。.
与平面BCD所成的角。. 因ADEF为正方形,AD=
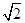 ,故EH=1,又EC=
,故EH=1,又EC=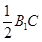 =2,
=2,所以∠ECH=300,即
 与平面BCD所成的角为300. 12分
与平面BCD所成的角为300. 12分解法二:
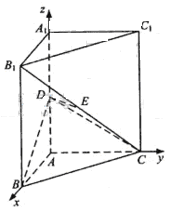
(1)以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A—xyz。
设B(1,0,0),C(0,b,0),D(0,0,c),则
 (1,0,2c),E(
(1,0,2c),E(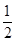 ,
,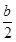 ,c).
,c).于是
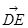 =(
=(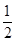 ,
,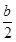 ,0),
,0),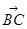 =(-1,b,0).由DE⊥平面
=(-1,b,0).由DE⊥平面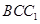 知DE⊥BC,
知DE⊥BC, 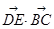 =0,求得b=1,所以 AB=AC。 5分
=0,求得b=1,所以 AB=AC。 5分(2)设平面BCD的法向量
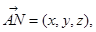 则
则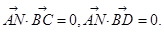
又
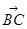 =(-1,1, 0),
=(-1,1, 0), =(-1,0,c),故
=(-1,0,c),故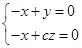
令x=1,则y=1,z=
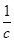 ,
,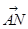 =(1,1,
=(1,1,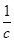 ).
).又平面
 的法向量
的法向量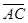 =(0,1,0)
=(0,1,0)由二面角
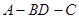 为60°知,
为60°知,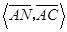 =60°,
=60°,故
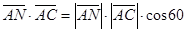 °,求得
°,求得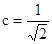 9分
9分于是
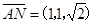 ,
, 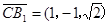
 ,
,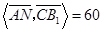 °
°所以
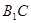 与平面
与平面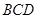 所成的角为30° 12分
所成的角为30° 12分
练习册系列答案
相关题目
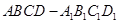 中,底面
中,底面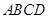 和侧面
和侧面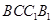 都
都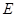 是
是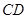 的中点,
的中点,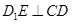 ,
,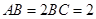 .
.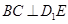
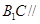 平面
平面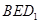 ;
;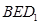 所成的锐二面角的大小为
所成的锐二面角的大小为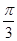 ,求线段
,求线段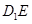 的长度.
的长度.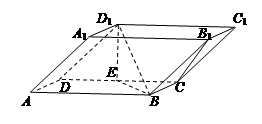

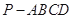 中,侧面
中,侧面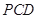
 底面
底面 ,
,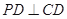 ,底面
,底面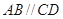 ,
,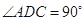 ,
,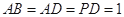 ,
,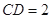 .
.
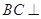 平面
平面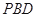 ;
;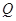 为侧棱
为侧棱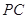 上一点,
上一点,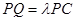 ,试确定
,试确定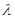 的值,使得二面角
的值,使得二面角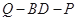 为
为 .
.
 是等腰梯形,
是等腰梯形,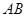 ∥
∥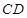 ,
, ,
,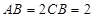 .在梯形
.在梯形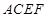 中,
中, ∥
∥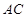 ,且
,且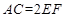 ,
,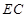 ⊥平面
⊥平面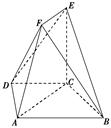
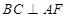 ;
; 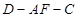 为
为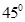 ,求
,求 的长.
的长.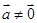 ,
,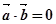 ,则
,则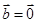 ; ②若
; ②若 ,则
,则 ;
;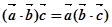 ; ④
; ④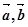 为非零不共线,若
为非零不共线,若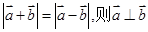 ;
;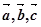 非零不共线,则
非零不共线,则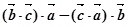 与
与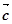 垂直
垂直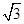 的正三角形,点S在底面ABC上的射影O恰是AC的中点,侧棱SB和底面成45°角.
的正三角形,点S在底面ABC上的射影O恰是AC的中点,侧棱SB和底面成45°角.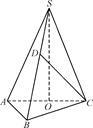
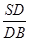 为何值时,CD⊥AB;
为何值时,CD⊥AB;