题目内容
17.已知正方形ABCD边长为16,取ABCD各边中点A1,B1,C1,D1,依次连接A1,B1,C1,D1,得到四边形A1B1C1D1,四边形A1B1C1D1内部的区域记作M1,再取四边形A1B1C1D1各边中点A2,B2,C2,D2,依次连接A2,B2,C2,D2,得到四边形A2B2C2D2,四边形A2B2C2D2内部含边界的区域记作M2,以此类推会得到区域M3,M4,M5,…,若在正方形ABCD内随机任取一点P,则点P取自区域M9的概率等于( )| A. | $\frac{1}{128}$ | B. | $\frac{1}{512}$ | C. | $\frac{1}{256}$ | D. | $\frac{1}{64}$ |
分析 由题意,本题是几何概型的概率,利用面积比得到所求.
解答 解:由题意,点P落在M9的概率等于其面积与大正方形的面积比,因为每次去中点得到的正方形面积是前一个面积的一半,所以M9的面积为$16×\frac{1}{{2}^{9}}$,
由几何概型的概率公式得到所求概率为$\frac{16×\frac{1}{{2}^{9}}}{16}=\frac{1}{512}$;
故选B.
点评 本题考查了几何概型的概率求法;关键是明确所求概率为面积比.

练习册系列答案
相关题目
8.已知a=0.7${\;}^{\frac{1}{8}}$,b=0.6${\;}^{-\frac{1}{8}}$,c=log20.5,则a,b,c的大小关系是( )
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | b<a<c |
9.命题“若m>0,则方程x2+x-m=0有实根”与其逆命题分别是( )
| A. | 真命题,真命题 | B. | 真命题,假命题 | C. | 假命题,真命题 | D. | 假命题,假命题 |
7.在某校开展的“阳光体育”系列活动中,甲、乙两班之间进行了一次200米跑的团体比赛.每个班各派出5名同学比赛,讲每名同学的200米成绩记录以后(单位:秒,且已知每个成绩都是整数),总用时少的班级获胜,
成绩记录如表所示:
表格中的x∈[30,40)
(1)若x=36,从甲班的5名同学中任取3名,记这3人中用时少于乙队平均用时的人数为随机变量η,求η的分布列;
(2)若最终乙班获胜,那么当乙班同学的成绩方差最大时,x的取值是多少(直接写出结果,不用证明)?
成绩记录如表所示:
| 队员编号 | 1 | 2 | 3 | 4 | 5 |
| 甲班成绩 | 31 | 34 | 33 | 29 | 28 |
| 乙班成绩 | 27 | 31 | 30 | X | 31 |
(1)若x=36,从甲班的5名同学中任取3名,记这3人中用时少于乙队平均用时的人数为随机变量η,求η的分布列;
(2)若最终乙班获胜,那么当乙班同学的成绩方差最大时,x的取值是多少(直接写出结果,不用证明)?
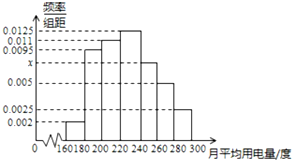 如图是某城市100户居民的月均用电量(单位:度)以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图.
如图是某城市100户居民的月均用电量(单位:度)以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图.