题目内容
已知函数f(x)=ax+
(x>1),若a是从0,1,2三数中任取一个,b是从1,2,3,4四数中任取一个,那么f(x)>b恒成立的概率为( )
| x |
| x-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:古典概型及其概率计算公式
专题:概率与统计
分析:由恒成立和分类讨论可得当a>0时有7种情况,当a=0时有1种情况,而总的共12种,由概率公式可得.
解答:
解析:当a>0时,由x>1知f(x)=ax+
=a(x-1)+
+a+1≥2
+a+1=(
+1)2,
∵f(x)>b恒成立,∵(
+1)2>b恒成立,
若b=1,则a=1,2;若b=2,则a=1,2;
若b=3,则a=1,2;若b=4,则a=2,共7种情况.
当a=0时,f(x)=
+1>1,b=1适合,
故所求概率为P=
=
.
故选:A
| x |
| x-1 |
=a(x-1)+
| 1 |
| x-1 |
| a |
| a |
∵f(x)>b恒成立,∵(
| a |
若b=1,则a=1,2;若b=2,则a=1,2;
若b=3,则a=1,2;若b=4,则a=2,共7种情况.
当a=0时,f(x)=
| 1 |
| x-1 |
故所求概率为P=
| 8 |
| 3×4 |
| 2 |
| 3 |
故选:A
点评:本题考查古典概型,涉及恒成立和分类讨论以及基本不等式,属中档题.

练习册系列答案
相关题目
求满足2x(2sinx-
)≥0,x∈(0,2π)的角α的集合( )
| 3 |
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
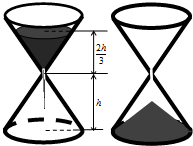 沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的
沙漏是古代的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图,某沙漏由上下两个圆锥组成,圆锥的底面直径和高均为8cm,细沙全部在上部时,其高度为圆锥高度的