题目内容
设函数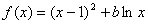 ,其中
,其中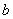 为常数。
为常数。
(Ⅰ)当 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(Ⅱ)若函数 有极值点,求
有极值点,求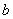 的取值范围及
的取值范围及 的极值点。
的极值点。
解:(Ⅰ)由题意知, 的定义域为
的定义域为 ,
,

∴当 时,
时, ,∴函数
,∴函数
 在定义域
在定义域 上单调递增.
上单调递增.
(Ⅱ)①由(Ⅰ)得,当 时,函数
时,函数 无极值点.
无极值点.
② 时,
时, 有两个相同的解
有两个相同的解 ,
,
但当 时,
时, ,当
,当 时,
时,
 时,函数
时,函数 在
在 上无极值点.
上无极值点.
③ 当
当 时,
时, 有两个不同解,
有两个不同解,


 时,
时, ,
,
而 ,
,
此时  ,
, 随
随 在定义域上的变化情况如下表:
在定义域上的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
| 减 | 极小值 | 增 |
由此表可知:当 时,
时, 有惟一极小值点
有惟一极小值点
ii) 当 时,0<
时,0< <1
<1
此时, ,
, 随
随 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 增 | 极大值 | 减 | 极小值 | 增 |
由此表 可知:
可知: 时,
时, 有一个极大值是
有一个极大值是
和一个极小值点 ;
;
综上所述:
当且仅当 时
时 有极值点;
有极值点;
当 时,
时, 有极小值点
有极小值点 ;没有极大值点
;没有极大值点
当 时,
时, 有一个极大值点
有一个极大值点 和一个极小值点
和一个极小值点

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目









 的前
的前 项和为
项和为 ,且
,且 ,则
,则 _____.
_____. ,且
,且 ,则
,则 的值为________.
的值为________.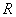 ,若存在常数
,若存在常数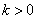 ,使
,使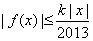 对于一切
对于一切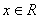 均成立,则称
均成立,则称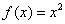 ; ②
; ②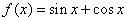 ;
; 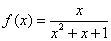 ; ④
; ④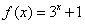 。其中
。其中 为△
为△ 外接圆的切线,
外接圆的切线, 的延长线交直线
的延长线交直线 ,
, 分别为弦
分别为弦 上的点,且
上的点,且 ,
, 四点共圆.若
四点共圆.若 ,则过
,则过 .
.

 ,则该几何体的俯视图可以是( )
,则该几何体的俯视图可以是( )

 上一点
上一点 到抛物线焦点的最短距离为1,则该抛物线的准线方程为 。
到抛物线焦点的最短距离为1,则该抛物线的准线方程为 。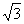 ,则异面直线AD,BC所成的角为( )
,则异面直线AD,BC所成的角为( )
 ,则a与b的夹角为( )
,则a与b的夹角为( )