题目内容
盒子里装有大小相同的 个球,其中
个球,其中 个
个 号球,
号球, 个
个 号球,
号球, 个
个 号球.
号球.
(Ⅰ)若第一次从盒子中任取一个球,放回后第二次再任取一个球,求第一次与第二次取到球的号码和是 的概率;
的概率;
(Ⅱ)若从盒子中一次取出 个球,记取到球的号码和为随机变量
个球,记取到球的号码和为随机变量 ,求
,求 的分布
的分布
列及期望.
[]
解:(Ⅰ)记“第一次与第二次取到的球上的号码的和是 ”为事件
”为事件 ,……… 1分
,……… 1分
则 ……… 4分
……… 4分
(Ⅱ) 可能取的值是
可能取的值是

 , ……… 5分
, ……… 5分
 , ……… 6分
, ……… 6分
 , ……… 7分
, ……… 7分
 , … 8分
, … 8分  . ……… 9分
. ……… 9分
∴ 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
……… 10分

故所求的数学期望为 . ……… 12分
. ……… 12分

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
一对父子参加一个亲子摸奖游戏,其规则如下:父亲在装有红色、白色球各两个的甲袋子里随机取两个球,儿子在装有红色、白色、黑色球各一个的乙袋子里随机取一个球,父子俩取球相互独立,两人各摸球一次合在一起称为一次摸奖,他们取出的 三个球的颜色情况与他们获得的积分对应如下表:
三个球的颜色情况与他们获得的积分对应如下表:
|

(Ⅰ)求一次摸奖中,所取的三个球中恰有两个是红球的概率;
(Ⅱ)设一次摸奖中,他们所获得的积分为X,求X的分布列及均值(数学期望)E(X);







 的定义域是 .
的定义域是 . ( )
( ) 上单调递增 B.在
上单调递增 B.在 上单调递增,在
上单调递增,在 上单调递减
上单调递减 上单调递减 D.在
上单调递减 D.在 上单调递减,在
上单调递减,在 上单调递增
上单调递增 的解集是
的解集是  B.
B. C.
C. D.
D.
 内任取一个实数
内任取一个实数 ,则使
,则使 与圆
与圆 无公共点的概率为 .
无公共点的概率为 .  的展开式中各
的展开式中各 项二项式系数和是16,则展开式中的常数项是____.
项二项式系数和是16,则展开式中的常数项是____. 表示的平面区域为
表示的平面区域为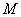 ,不等式
,不等式 表示的平面区域为
表示的平面区域为 .现随机向区域
.现随机向区域 ,满足
,满足 ,则
,则 的最小值是( )
的最小值是( ) B.
B. C.
C. D.
D.