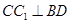题目内容
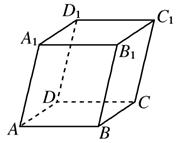
如图,平行六面体ABCD—A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°,则当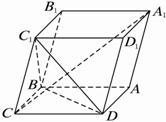
解析:设![]() =a,
=a,![]() =b,
=b,![]() =c,
=c,
由已知|a|=|b|,
![]() ·
·![]() =(a+ b+ c)(a-b)=|a|2-|b|2+a·c-b·c=|a||c|·cos60°-|b||c|·cos60°=0,
=(a+ b+ c)(a-b)=|a|2-|b|2+a·c-b·c=|a||c|·cos60°-|b||c|·cos60°=0,
∴CA1⊥BD.
因而A1C⊥平面C1BD的充要条件是CA1⊥C1D.
由![]() ⊥
⊥![]()
![]()
![]() ·
·![]() =(a+ b+ c)·(a-c)=0
=(a+ b+ c)·(a-c)=0![]() |a|2+a·b-b·c-|c|2=0?|a|2+|a|·|b|·cos60°-|b|·|c|·cos60°-|c|2=0
|a|2+a·b-b·c-|c|2=0?|a|2+|a|·|b|·cos60°-|b|·|c|·cos60°-|c|2=0![]() (3|a|+2|c|)·(|c|-|a|)=0.
(3|a|+2|c|)·(|c|-|a|)=0.
∵|a|>0,|c|>0,∴|a|=|c|.
∴当![]() =1时,A1C⊥平面C1BD.
=1时,A1C⊥平面C1BD.
温馨提示:这是条件开放性问题,从结论出发,利用向量垂直的条件由线线垂直推出线面垂直.本题通过利用向量的几何运算法则及向量的数量积运算大大降低了探索难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为
如图,平行六面体ANCD-EFGH中,棱AB,AD,AE的长分别为3,4,5,∠EAD=∠EAB=∠DAB=120°,则AG的长为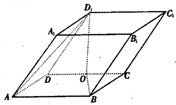 如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.
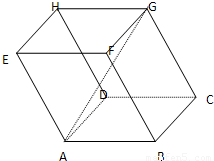
如图,平行六面体ABCD-A1B1C1D1中,AB=2,AD=1,底面ABCD是矩形,顶点D1在底面ABCD上的射影O恰好是CD的中点.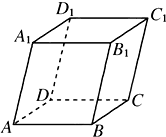 如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,
如图,平行六面体ABCD-A1B1C1D1中,∠BAD=∠BAA1=∠DAA1=60°,