题目内容

一个空间几何体
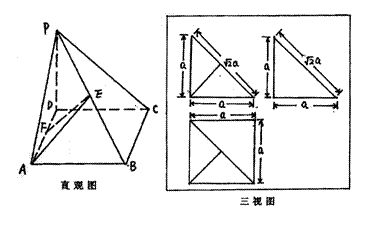
 的三视图如图所 示,其中
的三视图如图所 示,其中 分别是
分别是 五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形
五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形 为正方形且
为正方形且 ;在左视图中
;在左视图中 俯视图中
俯视图中 ,
,(Ⅰ)根据三视图作出空间几何体
 的直观图,并标明
的直观图,并标明 五点的位置;
五点的位置;(Ⅱ)在空间几何体
 中,过点
中,过点 作平面
作平面 的垂线,若垂足H在直线
的垂线,若垂足H在直线 上,求证:平面
上,求证:平面 ⊥平面
⊥平面 ;
;(Ⅲ)在(Ⅱ)的条件下,求三棱锥
 的体积及其外接球的表面积.
的体积及其外接球的表面积.平面 ⊥平面
⊥平面
 ⊥平面
⊥平面
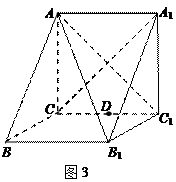
(Ⅰ)空间几何体的直观图如图所示,
且可得到平面 ⊥平面
⊥平面 ,
,
 四边形
四边形 为正方形且
为正方形且
(Ⅱ)证明: 过点
过点 作平面
作平面 的垂线,
的垂线,
垂足H在直线 上,
上,
 平面
平面 ,
,
 平面
平面 ,
, ,
,
又 平面
平面
 ⊥平面
⊥平面 ,
,
又 ,故平面
,故平面 ⊥平面
⊥平面
(Ⅲ)由(Ⅱ)知, ,
,

 为等腰直角三角形,
为等腰直角三角形,
过点 作
作 于点
于点 ,则
,则 ,
,

∴
取 的中点
的中点 ,由于
,由于 均为直角三角形,所以
均为直角三角形,所以


 是四棱锥
是四棱锥 的外接球的球心,半径为
的外接球的球心,半径为

且可得到平面
 ⊥平面
⊥平面 ,
, 四边形
四边形 为正方形且
为正方形且
(Ⅱ)证明:
 过点
过点 作平面
作平面 的垂线,
的垂线,垂足H在直线
 上,
上, 平面
平面 ,
, 平面
平面 ,
, ,
,又
 平面
平面
 ⊥平面
⊥平面 ,
,又
 ,故平面
,故平面 ⊥平面
⊥平面
(Ⅲ)由(Ⅱ)知,
 ,
,
 为等腰直角三角形,
为等腰直角三角形,过点
 作
作 于点
于点 ,则
,则 ,
,
∴

取
 的中点
的中点 ,由于
,由于 均为直角三角形,所以
均为直角三角形,所以

 是四棱锥
是四棱锥 的外接球的球心,半径为
的外接球的球心,半径为


练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
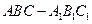 中,
中,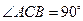 ,
,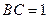 ,
,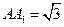 .
.
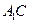
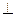 平面
平面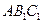 ;
;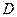 是棱
是棱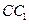 的中点,在棱
的中点,在棱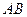 上是否存在一点
上是否存在一点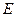 ,使
,使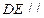 平面
平面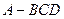 中,
中,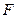 是
是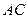 上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H
上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H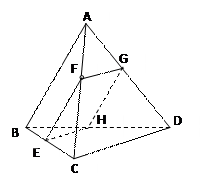
 中,
中, ,
,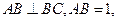
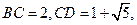 过
过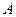 作
作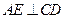 ,垂足为
,垂足为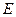 ,
,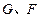 分别为
分别为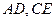 的中点,现将
的中点,现将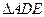 沿
沿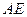 折叠使二面角
折叠使二面角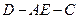 的平面角的正切值为
的平面角的正切值为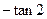 .
.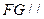 平面
平面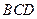 ;
;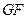 与
与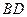 所成的角的余弦值;
所成的角的余弦值;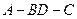 的大小.
的大小.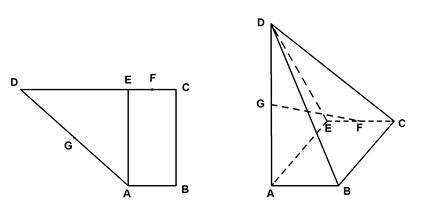
 8.
8. cm
cm
 cm
cm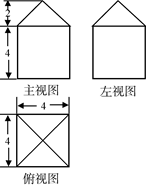
 中,
中, ,
, ,
, ,点
,点 在
在 上,且
上,且 .
. 平面
平面 ;
; 为棱,
为棱, 与
与 为面的二面角的大小.
为面的二面角的大小.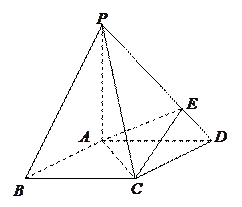
 ,这个长方体对角线的长是( )
,这个长方体对角线的长是( )


