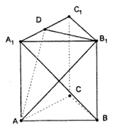
题目内容
如右图,在棱长都等于1的三棱锥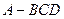 中,
中,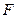 是
是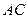 上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H
上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H
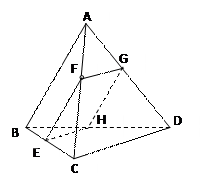
(1) 证明截面EFGH是矩形;
(2)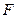 在
在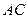 的什么位置时,截面面积最大,说明理由.
的什么位置时,截面面积最大,说明理由.
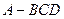 中,
中,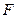 是
是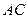 上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H
上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H
(1) 证明截面EFGH是矩形;
(2)
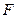 在
在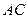 的什么位置时,截面面积最大,说明理由.
的什么位置时,截面面积最大,说明理由.(1)见解析(2)中点
(1)证:∵AB∥平面EFGH,
 平面ABC
平面ABC 平面EFGH=EF
平面EFGH=EF
∴AB∥EF
同理AB∥GH
∴EF∥GH
同理EH∥CD∥FG
∴四边形EFGH是平行四边形
取CD中点S,连接AS,BS
∵AC=AD,S是CD中点
∴AS⊥CD
同理 BS⊥CD
又∵AS BS=S
BS=S
∴CD⊥平面ABS
∴CD⊥AB 又∵AB∥EF,FG∥CD ∴EF⊥CD
即 四边形EFGH是矩形
(2) 设FG= ,
,
由(1)知 ,又CD=AB=1
,又CD=AB=1
∴EF=
则


∴当 时,
时, 最大
最大
即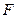 是
是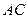 的中点时,截面面积最大
的中点时,截面面积最大
 平面ABC
平面ABC 平面EFGH=EF
平面EFGH=EF ∴AB∥EF
同理AB∥GH
∴EF∥GH
同理EH∥CD∥FG
∴四边形EFGH是平行四边形
取CD中点S,连接AS,BS
∵AC=AD,S是CD中点
∴AS⊥CD
同理 BS⊥CD
又∵AS
 BS=S
BS=S∴CD⊥平面ABS
∴CD⊥AB 又∵AB∥EF,FG∥CD ∴EF⊥CD
即 四边形EFGH是矩形
(2) 设FG=
 ,
,
由(1)知
 ,又CD=AB=1
,又CD=AB=1∴EF=

则



∴当
 时,
时, 最大
最大 即
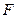 是
是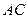 的中点时,截面面积最大
的中点时,截面面积最大 
练习册系列答案
相关题目
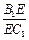 的值为多少时,
的值为多少时,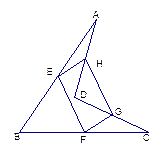

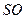 中,
中,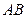 、
、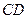 为底面圆的两条直径,
为底面圆的两条直径,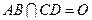 ,且
,且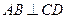 ,
,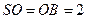 ,
,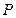 为
为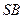 的中点.
的中点.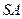 与
与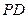 所成角的正切值.
所成角的正切值.

 的三视图如图所 示,其中
的三视图如图所 示,其中 分别是
分别是 五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形
五点在直立、侧立、水平三个投影面内的投影,且在主视图中,四边形 为正方形且
为正方形且 ;在左视图中
;在左视图中 俯视图中
俯视图中 ,
, 作平面
作平面 的垂线,若垂足H在直线
的垂线,若垂足H在直线 上,求证:平面
上,求证:平面 ⊥平面
⊥平面 ;
; 的体积及其外接球的表面积.
的体积及其外接球的表面积.
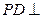 底面ABCD,PD=DC,E是PC的中点,作
底面ABCD,PD=DC,E是PC的中点,作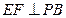 交PB于F.
交PB于F.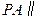 平面EDB;
平面EDB;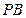
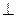 平面EFD.
平面EFD.
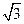
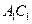
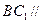 平面
平面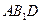
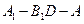 的大小
的大小