Question

(1)已知复数z满足|z－2－i|＝2，求复数w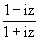＝的对应点的轨迹方程．

(2)连结椭圆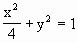的右焦点F与椭圆上的一动点P作正方形FPAB(F，P，A，B为顺时针方向排列)，求点P沿椭圆绕行一周时，B点的轨迹．

Answer 1

答案：
解析：

轨迹是以点(－1，－1)和点(－1，0)为端点的线段的中垂线2y＋1＝0． 　　(2)由题意可知F(，0)，设B(x，y)，P(2cosθ，sinθ)(0≤θ＜2π，x，y∈R)，F，P分别对应复数z＝和z＝2cosθ＋isinθ．B点对应复数z＝x＋yi，则由(－i)，即得x＋yi－＝(2cosθ－＋isinθ)(－i)，比较实虚部可得 (θ为参数)消去θ，得

提示：

注 利用复数的几何意义解轨迹问题有时很方便，特别是题设中以正方形、正三角形等为条件时，可利用复数乘法的几何意义来转化.