题目内容
20.已知二次函数f(x)=x2+2ax+2b有两个零点x1,x2,且-1<x1<1<x2<2,则直线bx-(a-1)y+3=0的斜率的取值范围是( )| A. | $(-\frac{2}{5},\frac{2}{3})$ | B. | $(-\frac{2}{5},\frac{3}{2})$ | C. | $(-\frac{2}{5},\frac{1}{2})$ | D. | $(-∞,-\frac{2}{5})∪(\frac{2}{3},+∞)$ |
分析 根据根的分布建立不等关系,画出满足条件的区域,明确目标函数的几何意义,即可求得结论.
解答 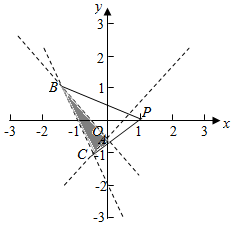 解:二次函数f(x)=x2+2ax+2b有两个零点x1,x2,
解:二次函数f(x)=x2+2ax+2b有两个零点x1,x2,
且-1<x1<1<x2<2,
则x1,x2是函数g(x)的两个零点,
∴$\left\{\begin{array}{l}{△=4{a}^{2}-8b>0}\\{f(-1)=1-2a+2b>0}\\{f(1)=1+2a+2b<0}\\{f(2)=4+4a+2b>0}\end{array}\right.$,其中△>0可以去掉.
画出可行域:平面三角形ABC的内部的所有点.
A(0,-$\frac{1}{2}$),B(-$\frac{3}{2}$,1),C(-$\frac{1}{2}$,-1).
直线bx-(a-1)y+3=0的斜率k=$\frac{b}{a-1}$,
表示经过两点(a,b),P(1,0)的直线的斜率.
kPC=$\frac{1}{1+\frac{1}{2}}$=$\frac{2}{3}$,kPB=$\frac{1}{-\frac{3}{2}-1}$=-$\frac{2}{5}$.
∴-$\frac{2}{5}$<k<$\frac{2}{3}$.
故选:A.
点评 本题考查解不等式、线性规划、二次函数的性质,考查了转化能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.已知变量x,y满足约束条件$\left\{\begin{array}{l}x-y≤0\\ x+y≤2\\ x≥0\end{array}\right.$,若 z=ax+y的最大值为4,则a=( )
| A. | 3 | B. | 2 | C. | -2 | D. | -3 |
8.已知i是虚数单位,且m(1+i)=7+ni(m,n∈R),则$\frac{m+ni}{2m-ni}$的虚部等于( )
| A. | $\frac{1}{7}$ | B. | $\frac{3}{14}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{5}$ |
12.设变量x,y满足约束条件 $\left\{\begin{array}{l}{x-y≤0}\\{x+y≥0}\\{x+2y≥0}\end{array}\right.$,则z=x-2y的最大值为0.
9.若直线y=k(x+2)上存在点(x,y)满足$\left\{\begin{array}{l}x-y≥0\\ x+y≤1\\ y≥-1\end{array}\right.$,则实数k的取值范围是( )
| A. | $[{-1,-\frac{1}{4}}]$ | B. | $[{-1,\frac{1}{5}}]$ | C. | $({-∞,-1}]∪[{\frac{1}{5},+∞})$ | D. | $[{-\frac{1}{4},\frac{1}{5}}]$ |
 如图,梯形ABCD中,AB∥CD,矩形BFED所在的平面与平面ABCD垂直,且AD=DC=CB=BF=$\frac{1}{2}$AB.
如图,梯形ABCD中,AB∥CD,矩形BFED所在的平面与平面ABCD垂直,且AD=DC=CB=BF=$\frac{1}{2}$AB.