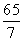题目内容
设数列{an}的前n项和为Sn，且S
－2Sn－anSn＋1＝0，n＝1，2，3，….
(1)求a1，a2，a3；
(2)求Sn的表达式．
解：(1)当n＝1时，由已知得a
－2a1－a＋1＝0，
解得a1＝
.
同理，可解得a2＝
，a3＝
.
(2)方法一：S－2Sn＋1－anSn＝0，
当n≥2(n∈N*)时，an＝Sn－Sn－1.
代入上式，得Sn－1Sn－2Sn＋1＝0(n≥2)．(*)
由(1)可得S1＝a1＝，S2＝a1＋a2＝＋＝
，
S3＝a1＋a2＋a3＝
.
所以当n＝k＋1时结论也成立．
练习册系列答案
相关题目
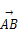=(2,4,0),
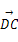=(-1,3,0),则异面直线AB与DC所成角θ的大小为
；
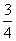＋C
>n
(n≥n0且n0∈N*)，则n的最小值为( )
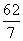B.
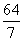D.