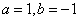题目内容
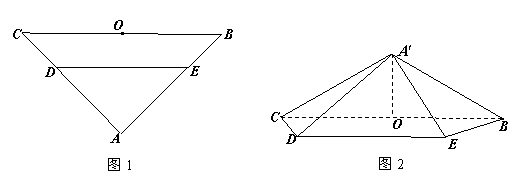
如图1,在等腰直角三角形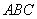 中,
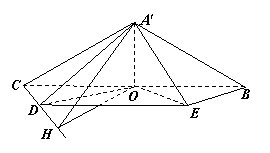
中, ,
, ,
,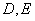 分别是
分别是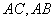 上的点,
上的点, ,
, 为
为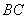 的中点.将
的中点.将 沿
沿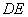 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥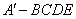 ,其中
,其中 .
.
(1) 证明: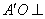 平面
平面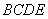 ;
;
(2) 求二面角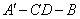 的平面角的余弦值.
的平面角的余弦值.

解:(1) 在图1中,易得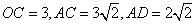


连结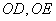 ,在
,在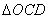 中,由余弦定理可得
中,由余弦定理可得
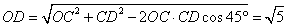
由翻折不变性可知 ,
,
所以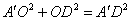 ,所以
,所以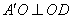 ,
,
理可证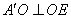 , 又
, 又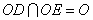 ,所以
,所以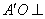 平面
平面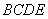 .
.
(2) 以 点为原点,建立空间直角坐标系
点为原点,建立空间直角坐标系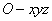 如图所示,
如图所示,
则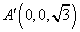 ,
,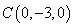 ,
,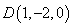
所以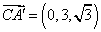 ,
,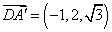
设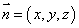 为平面
为平面 的法向量,则
的法向量,则
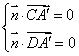 ,即
,即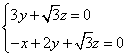 ,解得
,解得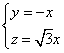 ,令
,令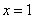 ,得
,得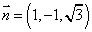
由(1) 知,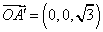 为平面
为平面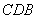 的一个法向量,
的一个法向量,
所以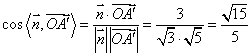 ,即二面角
,即二面角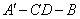 的平面角的余弦值为
的平面角的余弦值为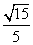 .
.

练习册系列答案
相关题目
总体由编号为01,02, ,19,20的20个个体组成,利用下面的随机数表选取6个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第6个个体的编号为( )
| 7816 | 6572 | 0802 | 6314 | 0702 | 4369 | 1128 | 0598 |
| 3204 | 9234 | 4935 | 8200 | 3623 | 4869 | 6938 | 7481 |
A.11 B.02 C.05 D.04
 的值,输出相应的
的值,输出相应的 的值,
的值,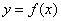 的解析式;
的解析式;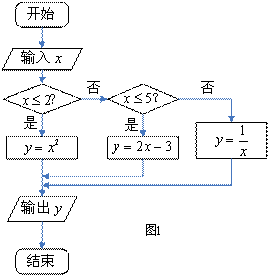
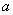 x-2在区间(1,+∞)内是增函数,则实数
x-2在区间(1,+∞)内是增函数,则实数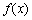 在定义域内可导,
在定义域内可导,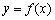 的图象如图1所示,则导函数
的图象如图1所示,则导函数 可能为 ( )
可能为 ( )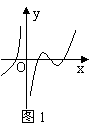
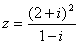 (i是虚数单位)在复平面上对应的点位于 ( )
(i是虚数单位)在复平面上对应的点位于 ( )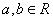 ,
,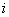 为虚数单位,且
为虚数单位,且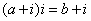 ,则( )
,则( )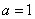 ,
,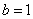 B.
B.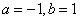 C.
C.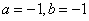 D.
D.