题目内容
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/小时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2 h追上,此时到达C处.
(1) 求渔船甲的速度;(2) 求sinα的值.
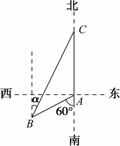
解:(1) 依题意知,∠BAC=120°,AB=12,AC=10×2=20,∠BCA=α.
在△ABC中,由余弦定理,得BC2=AB2+AC2-2AB·AC·cos∠BAC=122+202-2×12×20×cos120°=784,解得BC=28.
所以渔船甲的速度为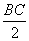 =14海里/小时.
=14海里/小时.
(2) 在△ABC中,因为AB=12海里,∠BAC=120°,BC=28海里,∠BCA=α,由正弦定理,得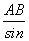 =
=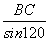 .
.
即sinα=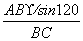 =
=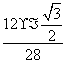 =
=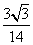 .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 ,则它的棱长为 .
,则它的棱长为 .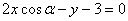 ,
, 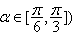 的倾斜角的变化范围是( )
的倾斜角的变化范围是( ) 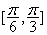 B.
B.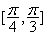 C.
C.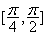 D.
D.
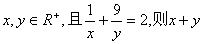 的最小值为______
的最小值为______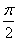 的是( )
的是( )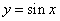 B.
B. C.
C.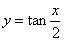 D.
D.
 的定义域是 .
的定义域是 .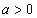 ,
, 满足约束条件
满足约束条件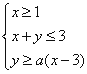 ,若
,若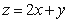 的最小值为
的最小值为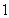 ,则
,则 ( )
( )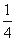 B.
B.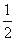 C.
C.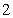
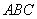 中,
中,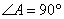 ,
,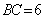 ,
,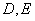 分别是
分别是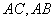 上的点,
上的点, ,
, 为
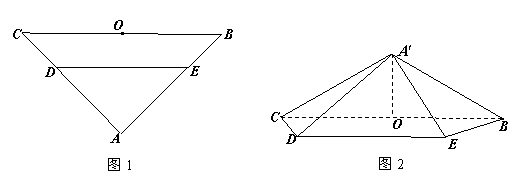
为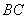 的中点.将
的中点.将 沿
沿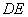 折起,得到如图2所示的四棱锥
折起,得到如图2所示的四棱锥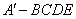 ,其中
,其中 .
.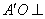 平面
平面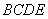 ;
; 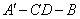 的平面角的余弦值.
的平面角的余弦值.