题目内容
7.已知全集U={0,1,2,3,4,5,6,7,8,9},集合$A=\{x|\sqrt{4x-{x^2}}>0,x∈N\}$,则集合∁UA中的元素个数为7.分析 由根式内部的代数式大于0求得x的范围化简A,再由补集运算得答案.
解答 解:由$A=\{x|\sqrt{4x-{x^2}}>0,x∈N\}$={x|0<x<4,且x∈N}={1,2,3},
又U={0,1,2,3,4,5,6,7,8,9},
得∁UA={0,4,5,6,7,8,9},
∴集合∁UA中的元素个数为7个.
故答案为:7.
点评 本题考查补集及其运算,考查了一元二次不等式的解法,是基础题.

练习册系列答案
相关题目
7.下列命题正确的是( )
| A. | 若a2>b2,则a>b | B. | 若ac>bc,则a>b | C. | 若$\frac{1}{a}>\frac{1}{b},则a<b$ | D. | 若$\sqrt{a}<\sqrt{b},则a<b$ |
18.已知f(x)(x∈R)有导函数,且?x∈R,f′(x)>f(x),n∈N*,则有( )
| A. | enf(-n)<f(0),f(n)>enf(0) | B. | enf(-n)<f(0),f(n)<enf(0) | ||
| C. | enf(-n)>f(0),f(n)>enf(0) | D. | enf(-n)>f(0),f(n)<enf(0) |
19.设a>0且a≠1,函数f(x)=loga|x2-(a+$\frac{1}{a}})x+1}$)x+1|在[1,2]上是增函数,则a的取值范围( )
| A. | a≥2+$\sqrt{3}$ | B. | 0<a<2-$\sqrt{3}$ | C. | a≥2+$\sqrt{3}$或0<a<1 | D. | a≥2+$\sqrt{3}$或0<a<2-$\sqrt{3}$ |
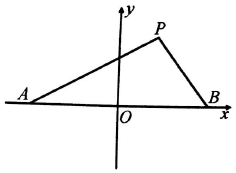 如图,设点A,B的坐标分别为(-$\sqrt{3}$,0),($\sqrt{3}$,0),直线AP,BP相交于点P,且它们的斜率之积为-$\frac{2}{3}$.
如图,设点A,B的坐标分别为(-$\sqrt{3}$,0),($\sqrt{3}$,0),直线AP,BP相交于点P,且它们的斜率之积为-$\frac{2}{3}$.