题目内容
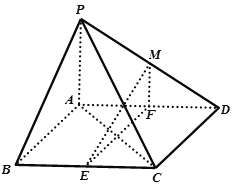
【题目】某大型商场为迎接新年的到来，在自动扶梯
的C点的上方悬挂竖直高度为5米的广告牌DE．如图所示，广告牌底部点E正好为DC的中点，电梯AC的坡度
．某人在扶梯上点P处(异于点C)观察广告牌的视角
．当人在A点时，观测到视角∠DAE的正切值为
．
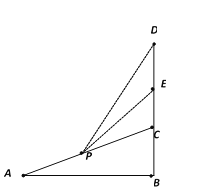
（1）求扶梯AC的长
（2）当某人在扶梯上观察广告牌的视角θ最大时，求CP的长．
【答案】（1）
；（2）
【解析】
（1）设
，用
分别表示出
和
，利用两角和的正切公式求出，再根据
的范围求解出答案；
（2）作
且交
于点
，设
，用分别表示出
和
，利用两角差的正切公式表示出
，利用基本不等式求出的最大值，此时
即
取最大值，利用基本不等式取最值的条件求出，再求出
即可.
（1）由题意，
为
的中点，
,所以
，
设，则
，
，
在
中，
，
在
中，
，
由两角和的正切公式，
，
，所以
，解得
，或
，
因为
，所以，
，
所以扶梯AC的长为米；
（2）作且交于点，如图所示，
设，则
，
，由（1）知，
，
，
，
当取最大值时，即取最大值，
，
当且仅当
，即
时等式成立，
所以此时
.
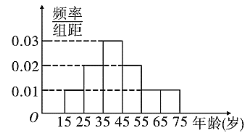
阅读快车系列答案
【题目】我市准备实施天然气价格阶梯制，现提前调查市民对天然气价格阶梯制的态度，随机抽查了
名市民，现将调查情况整理成了被调查者的频率分布直方图（如图）和赞成者的频数表如下：
年龄（岁） |
|
|
|
|
|
|
赞成人数 |
|
|
|
|
|
|
（1）若从年龄在
，
的被调查者中各随机选取
人进行调查，求所选取的
人中至少有
人对天然气价格阶梯制持赞成态度的概率；
（2）若从年龄在，
的被调查者中各随机选取人进行调查，记选取的人中对天然气价格实施阶梯制持不赞成态度的人数为
，求随机变量的分布列和数学期望.
【题目】某学校研究性学习小组对该校高二学生视力情况进行调查，学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有关系，对年级名次在1～50名和951～1000名的学生进行了调查，得到如下数据：
年级名次 是否近视 | 1～50 | 951～1000 |
近视 | 41 | 32 |
不近视 | 9 | 18 |
（1）根据表中的数据，能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系？
（2）在（1）中调查的100名学生中，按照分层抽样在不近视的学生中抽取了9人，进一步调查他们良好的护眼习惯，并且在这9人中任取3人，记名次在1～50名的学生人数为
，求的分布列和数学期望.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附：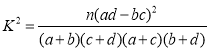
【题目】某种大型医疗检查机器生产商，对一次性购买2台机器的客户，推出两种超过质保期后两年内的延保维修优惠方案：方案一：交纳延保金7000元，在延保的两年内可免费维修2次，超过2次每次收取维修费2000元；方案二：交纳延保金10000元，在延保的两年内可免费维修4次，超过4次每次收取维修费1000元.某医院准备一次性购买2台这种机器。现需决策在购买机器时应购买哪种延保方案，为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数，得下表：
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 10 | 20 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率，记X表示这2台机器超过质保期后延保的两年内共需维修的次数。
（1）求X的分布列；
（2）以所需延保金及维修费用的期望值为决策依据，医院选择哪种延保方案更合算？