题目内容
已知函数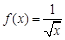 的定义域为集合
的定义域为集合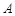 ,集合
,集合 ,
,
集合 .
.
(1)求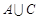 ;
;
(2)若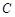
 (
( ),求
),求 的值.
的值.
(1) ,(2)1.
,(2)1.
解析试题分析:(1)求函数定义域,主要列出所有限制条件,本题一是要求分母不为零,二是要求偶次被开方数非负,结合两者得到函数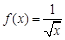 定义域为
定义域为 ;解对数不等式,注意真数要大于零及不等号的方向
;解对数不等式,注意真数要大于零及不等号的方向 =
= ,根据数轴求出集合的交集;(2)集合
,根据数轴求出集合的交集;(2)集合 是解参数不等式,由于参数
是解参数不等式,由于参数 大于零,所以先求出集合
大于零,所以先求出集合 为
为 ,再求出交集
,再求出交集 ,由
,由

 并结合数轴得
并结合数轴得 ,解此类问题需注意区间之间相互关系,并重视区间端点是否能取到.
,解此类问题需注意区间之间相互关系,并重视区间端点是否能取到.
试题解析:(1)由题意得 =
= .,
., =
= , 2分
, 2分
∴ . 4分
. 4分
(2)由题意得 =
= ,∴
,∴ , 6分
, 6分
∵

 , ∴
, ∴ , 8分
, 8分
∴ ,又∵
,又∵ , ∴
, ∴ =1. 10分
=1. 10分
考点:函数定义域,解对数不等式,集合运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. ;
; ,若
,若 恰有3个元素,求
恰有3个元素,求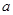 的取值范围.
的取值范围. ,集合
,集合 ,
,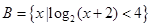 .
.
 ,若
,若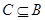 ,求实数
,求实数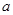 的取值范围.
的取值范围. ,集合
,集合 ,
, .
.
 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围. ,集合
,集合 .
. ;
; ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围. 的定义域为
的定义域为 ,集合
,集合 .
.  .
. ,
,
 ,;
,; ,若
,若 ,求实数
,求实数 的取值集合
的取值集合 ,函数
,函数 的定义域为集合
的定义域为集合 ,集合
,集合
 ;
; ,求实数
,求实数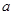 的范围.
的范围.