题目内容
设全集为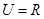 ,集合
,集合 ,
,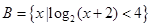 .
.
(1)求如图阴影部分表示的集合;
(2)已知 ,若
,若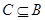 ,求实数
,求实数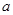 的取值范围.
的取值范围.
(1) (2)
(2)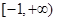
解析试题分析:(1)由图可知,阴影部分为 ,所以得找到集合
,所以得找到集合 ,根据已知解出集合
,根据已知解出集合 ,根据补集求得
,根据补集求得 ,然后可得阴影部分.
,然后可得阴影部分.
(2)因为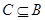 ,所以
,所以 ,故存在两种情况,得分别讨论,当
,故存在两种情况,得分别讨论,当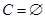 ,
, ,当
,当 时,
时, ,根据
,根据 是
是 的子集,所以集合
的子集,所以集合 的范围较小,可求出
的范围较小,可求出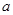 的范围.由于有两种情况,所以最后求.
的范围.由于有两种情况,所以最后求.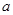 的并集.
的并集.
试题解析:(1)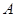 中,根据
中,根据 有
有
 中
中 ,则根据对数函数的单调性有
,则根据对数函数的单调性有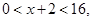
 所以
所以
阴影部分为
(2)因为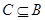 ,所以
,所以
①当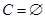 ,则
,则  ,即
,即 .
.
②当 时,
时, ,即
,即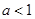 时,
时,
所以 得
得 .
.
综上所述,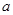 的取值范围为
的取值范围为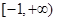 .
.
考点:集合的交并补运算,空集是任何集合的子集.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
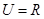 ,
,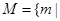 关于
关于 的方程
的方程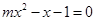 有实数根},
有实数根},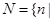 关于
关于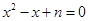 有实数根},
有实数根}, .
.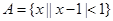 ,
,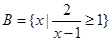 ,
, ,若“
,若“ ”是“
”是“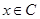 ”的充分不必要条件,求
”的充分不必要条件,求 的取值范围.
的取值范围.
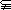 A∩B,A∩C=
A∩B,A∩C=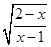 的定义域为集合
的定义域为集合 ,关于
,关于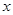 的不等式
的不等式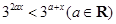 的解集为
的解集为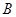 ,求使
,求使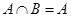 的实数
的实数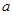 的取值范围.
的取值范围.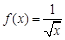 的定义域为集合
的定义域为集合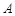 ,集合
,集合 ,
, .
.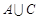 ;
;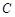
 (
( ),求
),求 的值.
的值.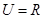 ,集合
,集合 ,
,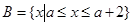 .
.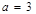 ,求
,求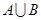 ,
,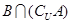 ;
; ,求
,求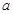 的范围.
的范围.