题目内容
4个男生和3个女生共7人，排成3列，不同的排法种类为（ ）
| A、（4!+3!）种 |
| B、7!种 |
| C、（4!×3!）种 |
| D、（4×3×3）种 |
考点：排列、组合及简单计数问题
专题：排列组合
分析：直接利用已知条件，通过排列求解即可．
解答：
解：7人排成3列，由于没有限制条件，可以看作是排成一列，所以不同的排法共有7!种方法．
故选：B．
故选：B．
点评：本题考查排列组合的应用，基本知识的考查．
练习册系列答案
相关题目
设θ为两个非零向量
，
的夹角，已知对任意实数t，|
+t
|的最小值为1（ ）
| a |
| b |
| b |
| a |
A、若|
| ||
B、若|
| ||
C、若θ确定，则|
| ||
D、若θ确定，则|
|
如果变量x，y满足约束条件
，则
的取值范围是（ ）
|
| 2y-2x-2 |
| 2x+1 |
A、[
| ||||
B、（-∞，
| ||||
C、（-∞，
| ||||
D、[
|
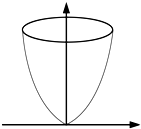抛物线y=x2（-2≤x≤2）绕y轴旋转一周形成一个如图所示的旋转体，在此旋转体内水平放入一个正方体，使正方体的一个面恰好与旋转体的开口面平齐，则此正方体的棱长是“3＜a＜4”是“函数f（x）=ax+3在（-1，2）上存在零点”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |