题目内容
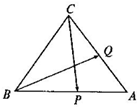如图，已知正三角形ABC的边长为1，点P是AB边上的动点，点Q是AC边上的动点，且| AP |
| AB |
| AQ |
| AC |
| BQ |
| CP |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由正三角形ABC的边长为1，可得
•
=1×1×cos60°．再利用向量的三角形法则可得
•
=(
+
)•(
+
)=[
+(1-λ)
]•(
+λ
)，利用数量积的性质展开，再利用二次函数的单调性即可得出．
| AB |
| AC |
| BQ |
| CP |
| BA |
| AQ |
| CA |
| AP |
| BA |
| AC |
| CA |
| AB |
解答：
解：∵正三角形ABC的边长为1，∴
•
=1×1×cos60°=
．
∴
•
=(
+
)•(
+
)
=[
+(1-λ)
]•(
+λ
)
=
•
-λ
2-（1-λ）
2+λ(1-λ)
•
=
-λ-（1-λ）+λ(1-λ)×
=-
(λ-
)2-
，
∵0≤λ≤1，
∴当λ=
时，
•
取得最大值-
．
故答案为：-
．
| AB |
| AC |
| 1 |
| 2 |
∴
| BQ |
| CP |
| BA |
| AQ |
| CA |
| AP |
=[
| BA |
| AC |
| CA |
| AB |
=
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
=
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
∵0≤λ≤1，
∴当λ=
| 1 |
| 2 |
| BQ |
| CP |
| 3 |
| 8 |
故答案为：-
| 3 |
| 8 |
点评：本题考查了正三角形的性质、向量的三角形法则、数量积的性质、二次函数的单调性等基础知识与基本技能方法，考查了推理能力和计算能力，属于中档题．
练习册系列答案
相关题目
若f（x）=-
x2+blnx在[1，+∞）上是减函数，则b的取值范围是（ ）
| 1 |
| 2 |
| A、[-1，+∞） |
| B、（-1，+∞） |
| C、（-∞，1] |
| D、（-∞，-1） |