解不等式|3x-1|＜x+2．题目和参考答案——青夏教育精英家教网—

题目内容

9．解不等式|3x-1|＜x+2．

分析把原不等式转化为不等式组$\left\{\begin{array}{l}{3x-1＜x+2}\\{3x-1＞-x-2}\end{array}\right.$，由此能求出结果．

解答解：∵|3x-1|＜x+2，
∴$\left\{\begin{array}{l}{3x-1＜x+2}\\{3x-1＞-x-2}\end{array}\right.$，
解得-$\frac{1}{4}＜x＜\frac{3}{2}$．
∴原不等式的解集为{x|-$\frac{1}{4}$＜x＜$\frac{3}{2}$}．

点评本题考查不等式的解法，是基础题，解题时要认真审题，注意含绝对值不等式的性质的合理运用．

练习册系列答案

20．

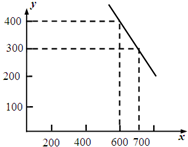某公司试销一种成本单价为500元/件的新产品，规定试销时销售单价不低于成本单价，又不高于800元/件．经试销调查，发现销售量y（件）与销售单价x（元/件）可近似看作一次函数y=kx+b的关系（如图所示）．
（1）由图象，求函数y=kx+b的表达式；
（2）设公司获得的毛利润（毛利润=销售总价-成本总价）为S元．试用销售单价x表示毛利润S，并求销售单价定为多少时，该公司获得最大毛利润？最大毛利润是多少？此时的销售量是多少？

17．有一个公用电话亭，里面有一部电话，在观察使用这部电话的人的流量时，设在某一时刻，有n个人正在使用电话或等待使用的概率为P（n），且P（n）与时刻t无关，统计得到P（n）=$\left\{\begin{array}{l}{（\frac{1}{2}）^{n}•P（0），1≤n≤6}\\{0，n≥7}\end{array}\right.$，那么在某一时刻，这个公用电话亭里一个人也没有的概率P（0）的值是$\frac{64}{127}$．

4．已知f（x）=x³+2xf′（1），则f′（1）=-3．

14．在△ABC中，若a=$\sqrt{3}$，b=$\sqrt{2}$，b=45°，则∠A的为（　　）

1．已知不等式ax²+ax+（a-1）≤0．
（1）当a=$\frac{1}{3}$，求不等式的解集；
（2）不等式的解集是不为空集，则a的取值范围．

18．已知幂函数f（x）=xⁿ的图象过点（8，$\frac{1}{4}$），且f（a+1）＜f（2），则a的范围是（　　）

19．用秦九韶算法计算多项式f（x）=x⁶-12x⁵+60x⁴-160x³+240x²-192x+64，当x=2时的值时，v₁的值为-10．

试题分类