题目内容
14.在△ABC中,若a=$\sqrt{3}$,b=$\sqrt{2}$,b=45°,则∠A的为( )| A. | 30°或120° | B. | 60°或120° | C. | 30° | D. | 60° |
分析 由已知利用正弦定理可求sinA的值,结合A的范围,利用特殊角的三角函数值即可得解.
解答 解:∵a=$\sqrt{3}$,b=$\sqrt{2}$,B=45°,
∴由正弦定理可得:sinA=$\frac{asinB}{b}$=$\frac{\sqrt{3}×\frac{\sqrt{2}}{2}}{\sqrt{2}}$=$\frac{\sqrt{3}}{2}$,
∵A∈(0°,180°),
∴A=60°,或120°.
故选:B.
点评 本题主要考查了正弦定理,特殊角的三角函数值在解三角形中的应用,考查了转化思想,属于基础题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
5.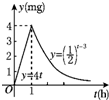 某医药研究所研发出一种新药,成年人按规定的剂量服用后,据检测,每毫升血液中的含药量y(mg)与时间t(h)之间的关系如图所示.据进一步测定,当每毫升血液中的含药量不少于0.25mg时,治疗疾病有效,则服药一次,治疗疾病有效的时间为( )
某医药研究所研发出一种新药,成年人按规定的剂量服用后,据检测,每毫升血液中的含药量y(mg)与时间t(h)之间的关系如图所示.据进一步测定,当每毫升血液中的含药量不少于0.25mg时,治疗疾病有效,则服药一次,治疗疾病有效的时间为( )
 某医药研究所研发出一种新药,成年人按规定的剂量服用后,据检测,每毫升血液中的含药量y(mg)与时间t(h)之间的关系如图所示.据进一步测定,当每毫升血液中的含药量不少于0.25mg时,治疗疾病有效,则服药一次,治疗疾病有效的时间为( )
某医药研究所研发出一种新药,成年人按规定的剂量服用后,据检测,每毫升血液中的含药量y(mg)与时间t(h)之间的关系如图所示.据进一步测定,当每毫升血液中的含药量不少于0.25mg时,治疗疾病有效,则服药一次,治疗疾病有效的时间为( )| A. | 4 h | B. | 4$\frac{7}{8}$ h | C. | 4$\frac{15}{16}$ h | D. | 5 h |
2.函数y=3-x(-2≤x≤1)的值域是( )
| A. | [3,9] | B. | [$\frac{1}{3}$,9] | C. | [$\frac{1}{3}$,3] | D. | [$\frac{1}{9}$,$\frac{1}{3}$] |
3.已知数列{an}为等比数列,则下列结论正确的是( )
| A. | a1+a3≥2a2 | B. | 若a3>a1,则a4>a2 | C. | 若a1=a3,则a1=a2 | D. | a12+a32≥2a22 |
4.已知集合A=﹛直线﹜,B=﹛双曲线﹜,则A∩B中元素个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 0或1或2 |
