题目内容
 已知A,B,C,D是函数y=sin(ωx+φ)一个周期内的图象上的四个点,如图所示,A(-
已知A,B,C,D是函数y=sin(ωx+φ)一个周期内的图象上的四个点,如图所示,A(-| π |
| 6 |
| CD |
| π |
| 12 |
A、ω=
| ||||
B、ω=
| ||||
C、ω=2,φ=
| ||||
D、ω=2,φ=
|
考点:y=Asin(ωx+φ)中参数的物理意义
专题:三角函数的图像与性质
分析:根据函数想性质得出最大值点的横坐标为
,A(-
,0),得出周期T=π,T=
,即可ω,运用A(-
,0),sin(-
+φ)=0,得出φ=kπ+
,k∈z,即可求解答案.
| π |
| 12 |
| π |
| 6 |
| 2π |
| ω |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
解答:
解:∵如图所示,A(-
,0),B为y轴上的点,C为图象上的最低点,
E为该函数图象的一个对称中心,B与D关于点E对称,
在△轴上的投影为
,
∴根据对称性得出:最大值点的横坐标为
,
∴
=
+
,T=π,
∵T=
∴ω=2,
∵A(-
,0),
∴sin(-
+φ)=0,
-
+φ=kπ,k∈z,
φ=kπ+
,k∈z,
∴φ=
,
故选:D
| π |
| 6 |
E为该函数图象的一个对称中心,B与D关于点E对称,
| CD |
| π |
| 12 |
∴根据对称性得出:最大值点的横坐标为
| π |
| 12 |
∴
| T |
| 4 |
| π |
| 6 |
| π |
| 12 |
∵T=
| 2π |
| ω |
∴ω=2,
∵A(-
| π |
| 6 |
∴sin(-
| π |
| 3 |
-
| π |
| 3 |
φ=kπ+
| π |
| 3 |
∴φ=
| π |
| 3 |
故选:D
点评:本题考查了三角函数的图象和性质,运用特殊点求解参变量的值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
过抛物线y2=4x的焦点F作两条互相垂直的直线l1,l2,l1交C于A、B,l2交C于M、N.则
+
=( )
| 1 |
| |AB| |
| 1 |
| |MN| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
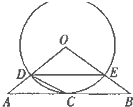 如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.
如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.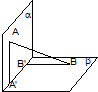 平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为
平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为