Question

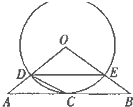如图，△ABO三边上的点C、D、E都在⊙O上，已知AB∥DE，AC=CB．
（l）求证：直线AB是⊙O的切线；
（2）若AD=2，且tan∠ACD=

1

2

，求⊙O的半径r的长．

Answer 1

考点：与圆有关的比例线段

专题：立体几何

分析：（1）如图所示，连接OC．由AB∥DE，可得

OA

OD

=

OB

OE

，由于OD=OE，可得OA=OB．由于AC=CB，可得OC⊥AB．即可得出直线AB是EO的切线．
（2）延长AO交⊙O于点F，连接CF．由（1）可得∠ACD=∠F．由tan∠ACD=

1

2

，可得tan∠F=

1

2

．由于△ACD∽△AFC，可得

CD

CF

=

AD

AC

=

1

2

，再利用切割线定理可得：AC²=AD•（AD+2r），即可得出．

解答： （1）证明：如图所示，连接OC．
∵AB∥DE，∴

OA

OD

=

OB

OE

，∵OD=OE，∴OA=OB．∵AC=CB，∴OC⊥AB．∴直线AB是EO的切线．
（2）解：延长AO交⊙O于点F，连接CF．由（1）可得∠ACD=∠F．
∵tan∠ACD=

1

2

，∴tan∠F=

1

2

．
∵△ACD∽△AFC，
∴

CD

CF

=

AD

AC

=

1

2

，
而AD=2，∴AC=4．
由切割线定理可得：AC²=AD•（AD+2r），
∴4²=2×（2+2r），解得r=3．

点评：本题考查了圆的切线的性质、切割线定理、相似三角形的性质、平行线分线段成比例定理，考查了推理能力与计算能力，属于中档题．