题目内容
19.在数列{an}中,a2=3且an+1+2an=0,则a1+a3的值是-$\frac{15}{2}$.分析 由题意可得数列{an}为以-2为公比的等比数列,再根据a2=3,即可求出答案.
解答 解:a2=3且an+1+2an=0,
∴an+1=-2an,
∴数列{an}为以-2为公比的等比数列,
∴a1+a3=$\frac{{a}_{2}}{q}$+a2q=$\frac{3}{-2}$+3×(-2)=-$\frac{15}{2}$,
故答案为:-$\frac{15}{2}$
点评 本题考查了等比数列的性质和定义,属于基础题.

练习册系列答案
相关题目
10.已知集合A={x|x-1<0},B={x∈N|x<4},则(∁RA)∩B=( )
| A. | {0} | B. | {1,2,3} | C. | {1} | D. | {1,2} |
2.等差数列{an}的前n项和为Sn,且$\frac{S_6}{S_3}=4$,则$\frac{S_9}{S_6}$=( )
| A. | $\frac{9}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{3}$ | D. | 4 |
 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,AP⊥BP,AC⊥BC,∠PAB=60°,∠ABC=45°,D是AB中点,E,F分别为PD,PC的中点.
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,AP⊥BP,AC⊥BC,∠PAB=60°,∠ABC=45°,D是AB中点,E,F分别为PD,PC的中点.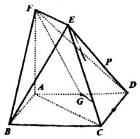 如图,正方形ABCD和梯形ACEF所在的平面相互垂直,EF∥AC,AF⊥AC,G为AD的中点,$AB=AF=2,EF=\sqrt{2}$.
如图,正方形ABCD和梯形ACEF所在的平面相互垂直,EF∥AC,AF⊥AC,G为AD的中点,$AB=AF=2,EF=\sqrt{2}$.