题目内容
如果关于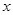 的不等式
的不等式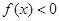 和
和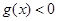 的解集分别为
的解集分别为 和
和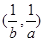 ,那么称这两个不等式为对偶不等式.如果不等式
,那么称这两个不等式为对偶不等式.如果不等式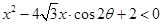 与不等式
与不等式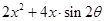
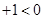 为对偶不等式,且
为对偶不等式,且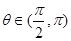 ,那么
,那么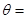 ______.
______.
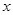 的不等式
的不等式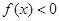 和
和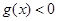 的解集分别为
的解集分别为 和
和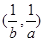 ,那么称这两个不等式为对偶不等式.如果不等式
,那么称这两个不等式为对偶不等式.如果不等式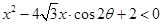 与不等式
与不等式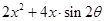
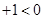 为对偶不等式,且
为对偶不等式,且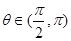 ,那么
,那么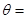 ______.
______.
试题分析:设
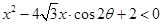 的解集为
的解集为 ,
, 的解集为
的解集为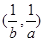 ,由二次方程根与系数的关系可得
,由二次方程根与系数的关系可得 ,
,
点评:二次不等式的解的边界值等于与之对应的二次方程的根,本题由不等式的解转化为方程的根,进而利用根与系数的关系找到有关于
 的关系式
的关系式
练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
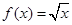 ,
,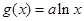 ,
,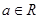
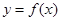 与曲线
与曲线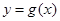 相交,且在交点处有相同的切线,求
相交,且在交点处有相同的切线,求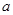 的值及该切线的方程;
的值及该切线的方程;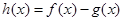 ,当
,当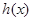 存在最小值时,求其最小值
存在最小值时,求其最小值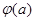 的解析式;
的解析式;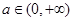 时,
时, 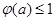 .
. 对任意
对任意 及
及 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )



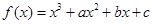 在
在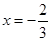 与
与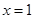 时都取得极值
时都取得极值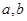 的值与函数
的值与函数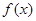 的单调区间
的单调区间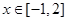 ,不等式
,不等式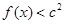 恒成立,求
恒成立,求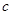 的取值范围。
的取值范围。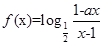 为奇函数,
为奇函数,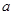 为常数,
为常数,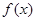 在区间
在区间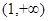 上单调递增;
上单调递增;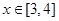 ,不等式
,不等式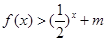 恒成立,求实数
恒成立,求实数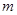 的取值范围。
的取值范围。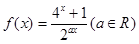 是偶函数,
是偶函数,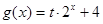 ,
,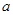 的值;(2)当
的值;(2)当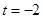 时,求
时,求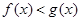 的解集;
的解集;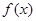 的图象总在
的图象总在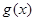 的图象上方,求实数
的图象上方,求实数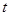 的取值范围.
的取值范围.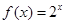 ,
,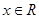 .
.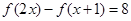 ;
;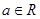 ,求函数
,求函数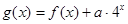 在区间
在区间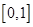 上的最大值
上的最大值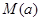 的表达式;
的表达式;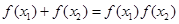 ,
,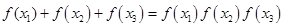 ,求
,求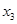 的最大值.
的最大值.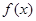 的定义域为
的定义域为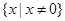 ,且满足对于定义域内任意的
,且满足对于定义域内任意的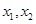 都有等式
都有等式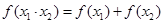 .
.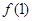 的值;
的值;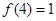 ,且
,且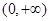 上是增函数,解关于
上是增函数,解关于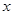 的不等式
的不等式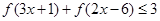 .
.