题目内容
已知函数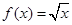 ,
,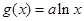 ,
,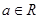
(Ⅰ)若曲线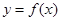 与曲线
与曲线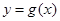 相交,且在交点处有相同的切线,求
相交,且在交点处有相同的切线,求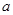 的值及该切线的方程;
的值及该切线的方程;
(Ⅱ)设函数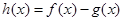 ,当
,当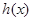 存在最小值时,求其最小值
存在最小值时,求其最小值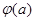 的解析式;
的解析式;
(Ⅲ)对(Ⅱ)中的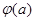 ,证明:当
,证明:当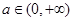 时,
时, 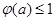 .
.
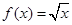 ,
,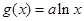 ,
,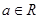
(Ⅰ)若曲线
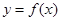 与曲线
与曲线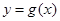 相交,且在交点处有相同的切线,求
相交,且在交点处有相同的切线,求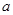 的值及该切线的方程;
的值及该切线的方程;(Ⅱ)设函数
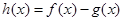 ,当
,当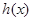 存在最小值时,求其最小值
存在最小值时,求其最小值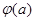 的解析式;
的解析式;(Ⅲ)对(Ⅱ)中的
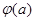 ,证明:当
,证明:当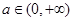 时,
时, 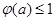 .
.(Ⅰ)a=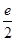 , y-e=
, y-e= (x-e2)(II)
(x-e2)(II)  (Ⅲ)利用函数的单调性证明
(Ⅲ)利用函数的单调性证明
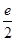 , y-e=
, y-e= (x-e2)(II)
(x-e2)(II)  (Ⅲ)利用函数的单调性证明
(Ⅲ)利用函数的单调性证明试题分析:(Ⅰ)
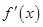 =
=
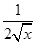 ,
,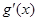 =
=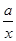 (x>0),
(x>0),由已知得
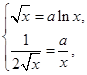 解得a=
解得a=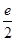 ,x=e2,
,x=e2,∴两条曲线交点的坐标为(e2,e) 切线的斜率为k=f’(e2)=

∴切线的方程为 y-e=
 (x-e2)
(x-e2)(II)由条件知h(x)=
 –aln x(x>0),
–aln x(x>0),(i)当a>0时,令
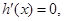 解得
解得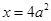 ,
,∴当0 <
 <
<  时,
时,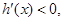 ,
,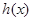 在(0,
在(0, )上递减;
)上递减;当x>
 时,
时,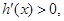 ,
,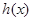 在
在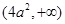 上递增.
上递增.∴
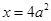 是
是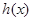 在
在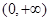 上的唯一极值点,且是极小值点,从而也是
上的唯一极值点,且是极小值点,从而也是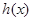 的最小值点.
的最小值点.∴最小值
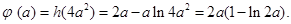
(ii)当
 时,
时,
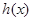 在(0,+∞)上递增,无最小值。
在(0,+∞)上递增,无最小值。故
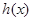 的最小值
的最小值 的解析式为
的解析式为
(Ⅲ)由(Ⅱ)知
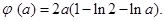
则
 ,令
,令 解得
解得 .
.当
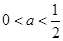 时,
时,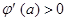 ,∴
,∴ 在
在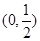 上递增;
上递增;当
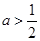 时,
时,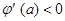 ,∴
,∴ 在
在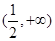 上递减.
上递减.∴
 在
在 处取得最大值
处取得最大值
∵
 在
在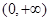 上有且只有一个极值点,所以
上有且只有一个极值点,所以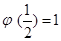 也是
也是 的最大值.
的最大值.∴当
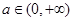 时,总有
时,总有
点评:导数本身是个解决问题的工具,是高考必考内容之一,高考往往结合函数甚至是实际问题考查导数的应用,求单调、最值、完成证明等,请注意归纳常规方法和常见注意点

练习册系列答案
相关题目
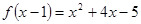 ,则
,则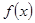 的表达式是 ___ .
的表达式是 ___ .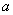 是实数.若函数
是实数.若函数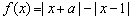 是定义在
是定义在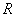 上的奇函数,但不是偶函数,则函数
上的奇函数,但不是偶函数,则函数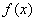 的递增区间为__________;
的递增区间为__________; 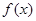 满足对于
满足对于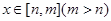 时有
时有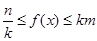 恒成立,则称函数
恒成立,则称函数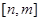 上是“被k限制”,若函数
上是“被k限制”,若函数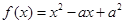 在区间
在区间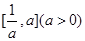 上是“被2限制”的,则
上是“被2限制”的,则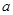 的取值范围为 .
的取值范围为 .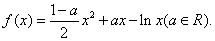
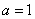 时,求函数
时,求函数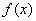 的极值;
的极值;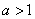 时,讨论函数
时,讨论函数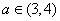 及任意
及任意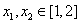 ,恒有
,恒有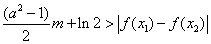 成立,求实数
成立,求实数 的取值范围.
的取值范围.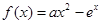
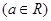 .
.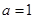 时,证明:
时,证明: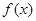 在
在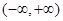 上为减函数;
上为减函数;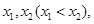 求实数
求实数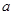 的取值范围.
的取值范围.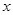 的不等式
的不等式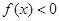 和
和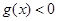 的解集分别为
的解集分别为 和
和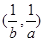 ,那么称这两个不等式为对偶不等式.如果不等式
,那么称这两个不等式为对偶不等式.如果不等式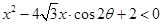 与不等式
与不等式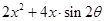
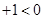 为对偶不等式,且
为对偶不等式,且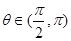 ,那么
,那么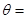 ______.
______.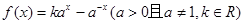 ,
,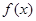 是定义域为R上的奇函数.
是定义域为R上的奇函数.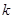 的值,并证明当
的值,并证明当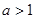 时,函数
时,函数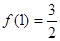 ,函数
,函数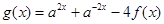 ,
,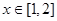 ,求
,求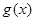 的值域;
的值域;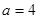 ,试问是否存在正整数
,试问是否存在正整数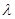 ,使得
,使得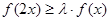 对
对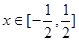 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数 ( )
( ) 上是单调增函数
上是单调增函数