题目内容
已知函数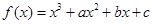 在
在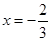 与
与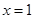 时都取得极值
时都取得极值
(1)求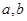 的值与函数
的值与函数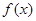 的单调区间
的单调区间
(2)若对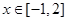 ,不等式
,不等式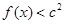 恒成立,求
恒成立,求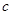 的取值范围。
的取值范围。
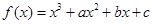 在
在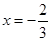 与
与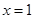 时都取得极值
时都取得极值(1)求
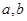 的值与函数
的值与函数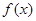 的单调区间
的单调区间(2)若对
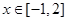 ,不等式
,不等式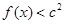 恒成立,求
恒成立,求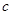 的取值范围。
的取值范围。(1)函数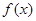 的递增区间是
的递增区间是 与
与 ,递减区间是
,递减区间是 ;
;
(2)
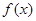 的递增区间是
的递增区间是 与
与 ,递减区间是
,递减区间是 ;
;(2)

试题分析:解:(1)

由
 ,
, 得
得
 ,函数
,函数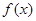 的单调区间如表:
的单调区间如表:  |  |  |  |  |  |
 |  |  |  |  |  |
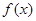 | | 极大值 | ¯ | 极小值 | |
 的递增区间是
的递增区间是 与
与 ,递减区间是
,递减区间是 ;
;(2)
 ,当
,当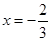 时,
时,
为极大值,而
 ,则
,则 为最大值,要使
为最大值,要使
恒成立,则只需要
 ,得
,得 。
。点评:主要是考查了导数的运用来求解单调性和最值的运用,属于基础题。

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案
相关题目
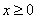 时,
时,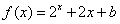 (
(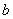 为常数),则
为常数),则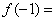 ( )
( )  ,则
,则 的值等于
的值等于 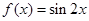 的图像向左平移
的图像向左平移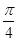 个单位,所得图像的解析式是( )
个单位,所得图像的解析式是( )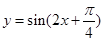
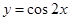
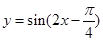
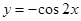
 上的函数
上的函数 满足下列三个条件:①对于任意的
满足下列三个条件:①对于任意的 都有
都有 ;②对于任意的
;②对于任意的 ;③函数
;③函数 的图象关于y轴对称,则下列结论正确的是 ( )
的图象关于y轴对称,则下列结论正确的是 ( )



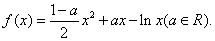
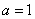 时,求函数
时,求函数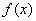 的极值;
的极值;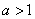 时,讨论函数
时,讨论函数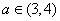 及任意
及任意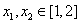 ,恒有
,恒有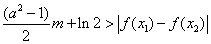 成立,求实数
成立,求实数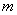 的取值范围.
的取值范围.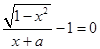 仅有一解,则实数
仅有一解,则实数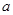 的取值范围是 .
的取值范围是 .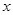 的不等式
的不等式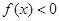 和
和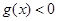 的解集分别为
的解集分别为 和
和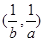 ,那么称这两个不等式为对偶不等式.如果不等式
,那么称这两个不等式为对偶不等式.如果不等式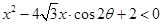 与不等式
与不等式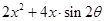
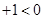 为对偶不等式,且
为对偶不等式,且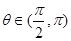 ,那么
,那么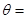 ______.
______. 满足:①定义域为
满足:①定义域为 ;②对任意
;②对任意 ,有
,有 ;③当
;③当 时,
时, .记
.记 ,根据以上信息,可以得到函数
,根据以上信息,可以得到函数 在区间
在区间 内的零点个数是___ ___.
内的零点个数是___ ___.