题目内容
8.若loga$\frac{3}{2}$<1,则a的取值范围是a>$\frac{3}{2}$或0<a<1.分析 先把1变成底数的对数,再讨论底数与1的关系,确定函数的单调性,根据函数的单调性整理出关于a的不等式,得到结果,把两种情况求并集得到结果.
解答 解:∵loga$\frac{3}{2}$<1,
∴loga$\frac{3}{2}$<1=logaa,
当a>1时,函数是一个增函数,不等式的解是a>$\frac{3}{2}$;
当0<a<1时,函数是一个减函数,根据函数的单调性有loga$\frac{3}{2}$<0<1成立;
综上可知a的取值是a>$\frac{3}{2}$或0<a<1.
故答案为:a>$\frac{3}{2}$或0<a<1.
点评 本题主要考查对数函数单调性的应用、不等式的解法等基础知识,本题解题的关键是对于底数与1的关系,这里应用分类讨论思想来解题.

练习册系列答案
相关题目
19.已知命题p;对?x∈R,?m0∈R.使4x+2xm0+1=0.若命题¬p是假命题.则实数m0的取值范围是( )
| A. | .[-2,2] | B. | .[2,+∞) | C. | (-∞,-2] | D. | [-2,+∞) |
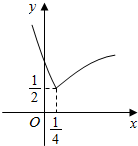 如图所示的函数F(x)的图象是由指数函数f(x)=ax(a>0且a≠1)与幂函数g(x)=xa“拼接“而成的,则下列四个数中最大的是( )
如图所示的函数F(x)的图象是由指数函数f(x)=ax(a>0且a≠1)与幂函数g(x)=xa“拼接“而成的,则下列四个数中最大的是( )