题目内容
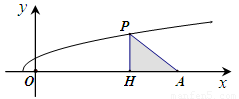
如图,已知点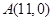 ,函数
,函数 的图象上的动点
的图象上的动点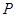 在
在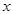 轴上的射影为
轴上的射影为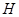 ,且点
,且点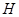 在点
在点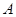 的左侧.设
的左侧.设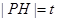 ,
,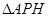 的面积为
的面积为 .
.
(Ⅰ)求函数 的解析式及
的解析式及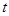 的取值范围;
的取值范围;
(Ⅱ)求函数 的最大值.
的最大值.
【答案】
(Ⅰ) ;(Ⅱ)8.
;(Ⅱ)8.
【解析】
试题分析:(Ⅰ)根据已知条件,需要表示出 和
和 ,因为
,因为 ,所以点
,所以点 的横坐标为
的横坐标为 ,
,
而 在点
在点 的左侧,所以
的左侧,所以 ,即
,即 ,由已知
,由已知 ,所以
,所以 ,则
,则 所以
所以 的面积为
的面积为 ;(Ⅱ)
;(Ⅱ) 是关于t的三次函数,要求它的最大值,用导数的方法求解,
是关于t的三次函数,要求它的最大值,用导数的方法求解, ,由
,由 ,得
,得 (舍),或
(舍),或 .
根据函数单调性情况,知当
.
根据函数单调性情况,知当 时,函数
时,函数 取得最大值8.
取得最大值8.
试题解析:(Ⅰ)由已知可得 ,所以点
,所以点 的横坐标为
的横坐标为 ,
,
因为点 在点
在点 的左侧,所以
的左侧,所以 ,即
,即 .
.
由已知 ,所以
,所以 ,
,
所以
所以 的面积为
的面积为 .
.
(Ⅱ)
由 ,得
,得 (舍),或
(舍),或 .
.
函数 与
与 在定义域上的情况如下:
在定义域上的情况如下:
|
|
|
2 |
|
|
|
+ |
0 |
|
|
|
↗ |
极大值 |
↘ |
所以当 时,函数
时,函数 取得最大值8.
取得最大值8.
考点:1.利用导数求函数最值.

练习册系列答案
相关题目




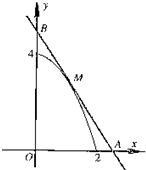 如图,已知M是函数y=4-x2(1<x<2)的图象C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A,B,O是坐标原点,求△AOB面积的最小值.
如图,已知M是函数y=4-x2(1<x<2)的图象C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A,B,O是坐标原点,求△AOB面积的最小值.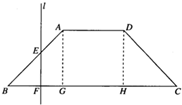 如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为
如图,已知底角为45°的等腰梯形ABCD,底边BC长为7cm,腰长为 如图,已知点A(11,0),直线x=t(-1<t<11)与函数
如图,已知点A(11,0),直线x=t(-1<t<11)与函数