题目内容
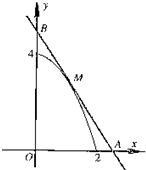如图，已知M是函数y=4-x2（1＜x＜2）的图象C上一点，过M点作曲线C的切线与x轴、y轴分别交于点A，B，O是坐标原点，求△AOB面积的最小值．
分析：因为M是函数y=4-x2（1＜x＜2）的图象C上一点，设出M的坐标，利用y′求出过M点曲线C的切线斜率k并写出切线方程，就能得到A和B两点的坐标，根据
得出三角形的面积与m的函数关系式S，令S′=0求出稳定点，在0＜m＜2区间内分区间讨论函数的增减性，最后求出S的最小值即可．
| OA×OB |
| 2 |
解答：解：∵y=4-x2
∴y'=-2x．
设M（m，4-m2），则过M点曲线C的切线斜率k=-2m．
∴切线方程y-（4-m2）=-2m（x-m）． 由x=0，得y=4+m2，B（0，4+m2）．由y=0x=
，A(
，0)，其中0＜m＜2.设△AOB的面积为S，则S=S=
|4+m2|•|
|=
=
，(0＜m＜2).
∴S′=
=
.
令S′=0，得3m4+8m2-16=0，解得m=
∈(0，2).
当m∈(0，
)时，S′＜0，S在区间(0，
)上为减函数；
当m∈(
，2)时，S′＞0，S在区间(
，2)上为增函数；
∴当m=
时S取得最小值，最小值为Smin=S(
)=
.
∴y'=-2x．
设M（m，4-m2），则过M点曲线C的切线斜率k=-2m．
∴切线方程y-（4-m2）=-2m（x-m）． 由x=0，得y=4+m2，B（0，4+m2）．由y=0x=
| 4+m2 |
| 2m |
| 4+m2 |
| 2m |
| 1 |
| 2 |
| 4+m2 |
| 2m |
| (4+m2)2 |
| 4m |
| m4+8m2+16 |
| 4m |
∴S′=
| (4m3+16m)m-(m4+8m2+16) |
| 4m2 |
| 3m4+8m2-16 |
| 4m2 |
令S′=0，得3m4+8m2-16=0，解得m=
2
| ||
| 3 |
当m∈(0，
2
| ||
| 3 |
2
| ||
| 3 |
当m∈(
2
| ||
| 3 |
2
| ||
| 3 |
∴当m=
2
| ||
| 3 |
2
| ||
| 3 |
32
| ||
| 9 |
点评：本题考查曲线切线方程的写法以及导数为零时函数的稳定点判断函数的增减性，在闭区间利用导数求最值的方法．
练习册系列答案
相关题目
