题目内容
14.下列命题中正确的个数是( )①若λ$\overrightarrow{a}$+μ$\overrightarrow{b}$=$\overrightarrow{0}$,则λ=μ=0;
②若$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$在$\overrightarrow{b}$的投影为|$\overrightarrow{a}$|;
③若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则$\overrightarrow{a}$•$\overrightarrow{b}$=($\overrightarrow{a}$•$\overrightarrow{b}$)2;
④tan40°tan15°+tan15°tan35°+tan35°tan40°=1;
⑤cos$\frac{π}{7}$cos$\frac{2π}{7}$cos$\frac{4π}{7}$=-$\frac{1}{8}$;
⑥在△ABC中,若sinC=2cosAsinB,则△ABC一定是等腰三角形.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 讨论向量共线和不共线,即可判断①;讨论向量同向共线和反向共线,即可判断②;
由向量垂直的条件:数量积为0,即可判断③;运用两角和的正切公式的变形,即可判断④;
运用二倍角的正弦公式和诱导公式,即可判断⑤;运用诱导公式和两角和的正弦公式,即可判断⑥.
解答 解:对于①,当$\overrightarrow{a}$,$\overrightarrow{b}$不共线时,若λ$\overrightarrow{a}$+μ$\overrightarrow{b}$=$\overrightarrow{0}$,则λ=μ=0,故①错误;
对于②,当向量$\overrightarrow{a}$,$\overrightarrow{b}$同向时,则$\overrightarrow{a}$在$\overrightarrow{b}$的投影为|$\overrightarrow{a}$|,故②错误;
对于③,若$\overrightarrow{a}$⊥$\overrightarrow{b}$,即有$\overrightarrow{a}$•$\overrightarrow{b}$=0,则$\overrightarrow{a}$•$\overrightarrow{b}$=($\overrightarrow{a}$•$\overrightarrow{b}$)2,故③正确;
对于④,tan40°tan15°+tan15°tan35°+tan35°tan40°=tan15°(tan40°+tan35°)+
tan35°tan40°=tan15°tan75°(1-tan35°tan40°)+tan35°tan40°=1-tan35°tan40°
+tan35°tan40°=1,故④正确;
对于⑤,cos$\frac{π}{7}$cos$\frac{2π}{7}$cos$\frac{4π}{7}$=$\frac{1}{2}$•2sin$\frac{π}{7}$cos$\frac{π}{7}$cos$\frac{2π}{7}$cos$\frac{4π}{7}$•$\frac{1}{sin\frac{π}{7}}$=$\frac{1}{2}$sin$\frac{2π}{7}$cos$\frac{2π}{7}$cos$\frac{4π}{7}$•$\frac{1}{sin\frac{π}{7}}$
=$\frac{1}{4}$sin$\frac{4π}{7}$cos$\frac{4π}{7}$•$\frac{1}{sin\frac{π}{7}}$=$\frac{1}{8}$sin$\frac{8π}{7}$•$\frac{1}{sin\frac{π}{7}}$=-$\frac{1}{8}$,故⑤正确;
对于⑥,在△ABC中,若sinC=2cosAsinB,即为sin(A+B)=sinAcosB+cosAsinB=2cosAsinB,
即有tanA=tanB,可得A=B,则△ABC一定是等腰三角形,故⑥正确.
综上可得,正确的个数为4.
故选:C.
点评 本题考查向量的共线和数量积的性质的运用,考查三角函数的化简求值,注意运用两角和的正弦公式和二倍角公式,考查三角形的形状的判断,属于中档题.

| A. | (kπ-$\frac{π}{2}$,kπ+$\frac{π}{2}$),k∈Z | B. | (kπ,(k+1)π),k∈Z | ||
| C. | (kπ-$\frac{3π}{4}$,kπ+$\frac{π}{4}$),k∈Z | D. | (kπ-$\frac{π}{4}$,kπ+$\frac{3π}{4}$),k∈Z |
| A. | $\overrightarrow{AB}$=$\overrightarrow{BC}$+$\overrightarrow{CD}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{DC}$+$\overrightarrow{BC}$=$\overrightarrow{AD}$ | C. | $\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{DC}$ | D. | $\overrightarrow{BC}$=$\overrightarrow{BD}$-$\overrightarrow{DC}$ |
| A. | 0.43<30.4<log43 | B. | log43<0.43<30.4 | C. | 0.43<log43<30.4 | D. | log43<30.4<0.43 |
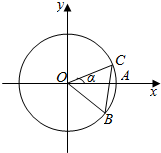 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为( )| A. | $\frac{5}{13}$ | B. | $\frac{12}{13}$ | C. | -$\frac{5}{13}$ | D. | -$\frac{12}{13}$ |
| A. | {1,5} | B. | {1,2,5} | C. | {2,3} | D. | {1,2,3,5} |