题目内容
在△ABC，内角A，B，C的对边分别为a，b，c．已知∠B为锐角，b=7，ac=40，△ABC外接圆半径为
，求sinA的值．
7
| ||
| 3 |
考点：正弦定理
专题：解三角形
分析：由正弦定理可得：
=2R，解得B=
．由余弦定理可得：b2=a2+c2-2accosB，与ac=40联立，解得a，再利用正弦定理即可得出．
| b |
| sinB |
| π |
| 3 |
解答：
解：由正弦定理可得：
=2R，∴sinB=
=
，
∵∠B为锐角，∴B=
．
由余弦定理可得：b2=a2+c2-2accosB，
∴72=a2+c2-ac，即a2+c2-ac=49．
与ac=40联立，解得a=5或8．
∴
=2R，
∴sinA=
=
或
．
| b |
| sinB |
| 7 | ||||
2×
|
| ||
| 2 |
∵∠B为锐角，∴B=
| π |
| 3 |
由余弦定理可得：b2=a2+c2-2accosB，
∴72=a2+c2-ac，即a2+c2-ac=49．
与ac=40联立，解得a=5或8．
∴
| a |
| sinA |
∴sinA=
| a |
| 2R |
5
| ||
| 14 |
8
| ||
| 14 |
点评：本题查克拉正弦定理、余弦定理，考查了推理能力与计算能力，属于中档题．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
相关题目
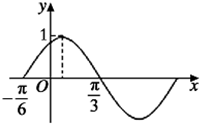如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜