题目内容
已知二次函数f(x)=ax2+bx+1开口向上,g(x)=log
f(x).
(1)令b=-3,若g(x)在x∈[1,2]上单凋递减,求a的取值范围;
(2)若f(x+2)为偶函数,定义区间[m,n]的长度为n-m,问是否存在常数a,使得函数y=f(x)在区间[a,3]且a≥1的值域为D,且D的长度为10-a2?若存在,求出a的值,若不存在,请说明理由.
| 1 |
| 2 |
(1)令b=-3,若g(x)在x∈[1,2]上单凋递减,求a的取值范围;
(2)若f(x+2)为偶函数,定义区间[m,n]的长度为n-m,问是否存在常数a,使得函数y=f(x)在区间[a,3]且a≥1的值域为D,且D的长度为10-a2?若存在,求出a的值,若不存在,请说明理由.
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:(1)由题意,f(x)=ax2-3x+1,a>0,由复合函数的单调性知,f(x)在x∈[1,2]上单凋递增,且f(1)>0,从而解得;
(2)由f(x+2)为偶函数可得f(x)关于x=2对称,从而得到f(x)=a(x-2)2-4a+1,讨论对称轴与区间[a,3]的位置关系,从而确定值域D,进而求D的长度为10-a2时a的值.
(2)由f(x+2)为偶函数可得f(x)关于x=2对称,从而得到f(x)=a(x-2)2-4a+1,讨论对称轴与区间[a,3]的位置关系,从而确定值域D,进而求D的长度为10-a2时a的值.
解答:
解:(1)由题意,f(x)=ax2-3x+1,a>0;
又∵g(x)在x∈[1,2]上单凋递减,
∴f(x)在x∈[1,2]上单凋递增,且f(1)>0,
即
,
解得a>2;
(2)∵f(x+2)为偶函数,
∴f(x)关于x=2对称,
故-
=2,解得,4a+b=0;
f(x)=a(x-2)2-4a+1,
假设存在常数a,
则若1≤a≤2,
则fmin(x)=-4a+1,fmax(x)=f(3)=-3a+1,
则-3a+1-(-4a+1)=10-a2,
即a2+a-10=0,在[1,2]上无解;
若2<a<3,
则fmin(x)=f(a)=a3-4a2+1,fmax(x)=f(3)=-3a+1,
则-3a+1-(a3-4a2+1)=10-a2,
即a3-5a2+3a+10=0,
作函数F(a)=a3-5a2+3a+10的图象如下,

故不存在.
又∵g(x)在x∈[1,2]上单凋递减,
∴f(x)在x∈[1,2]上单凋递增,且f(1)>0,
即
|
解得a>2;
(2)∵f(x+2)为偶函数,
∴f(x)关于x=2对称,
故-
| b |
| 2a |
f(x)=a(x-2)2-4a+1,
假设存在常数a,
则若1≤a≤2,
则fmin(x)=-4a+1,fmax(x)=f(3)=-3a+1,
则-3a+1-(-4a+1)=10-a2,
即a2+a-10=0,在[1,2]上无解;
若2<a<3,
则fmin(x)=f(a)=a3-4a2+1,fmax(x)=f(3)=-3a+1,
则-3a+1-(a3-4a2+1)=10-a2,
即a3-5a2+3a+10=0,
作函数F(a)=a3-5a2+3a+10的图象如下,

故不存在.
点评:本题考查了二次函数的性质应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)=(a2-2a-3)x2+(a-3)x+1的定义域和值域都为R,则( )
| A、a=-1或a=3 | B、a=-1 |
| C、a=3 | D、a不存在 |
设集合A={α|α=k•180°+90°,k∈z}∪{α|α=k•180°,k∈z},集合B={β|β=k•90°,k∈z},则( )
| A、A?B | B、A?B |
| C、A∩B=∅ | D、A=B |
在△ABC中,角A、B、C所对的边分别为a,b,c,若
•
=
•
=1,那么c等于( )
| AB |
| AC |
| BA |
| BC |
| A、2 | ||
B、
| ||
C、
| ||
| D、4 |
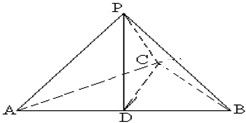 如图,已知三棱锥P-ABC,D为AB的中点,且△PDB是正三角形,PA⊥PC.求证:PC⊥BC.
如图,已知三棱锥P-ABC,D为AB的中点,且△PDB是正三角形,PA⊥PC.求证:PC⊥BC.