题目内容
如图,在平行四边形ABCD中,CD=1,∠BCD=60°,且BD⊥CD,正方形ADEF所在平面与平面ABCD垂直,G、H分别是DF、BE的中点。

(1)求证:BD⊥平面CDE;
(2)求证:GH∥平面CDE;
(3)求三棱锥D-CEF的体积。
(2)求证:GH∥平面CDE;
(3)求三棱锥D-CEF的体积。
解:(1)∵四边形ADEF是正方形,
∴ED⊥AD
又平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,
∴ED⊥平面ABCD
∴ED⊥BD
又BD⊥CD,且ED∩DC=D,
∴BD⊥平面CDE。
(2)∵G为DF的中点,且易知H是FC的中点,
则在△FCD中,GH∥CD
又∵CD 平面CDE,GH
平面CDE,GH 平面CDE,
平面CDE,
∴GH∥平面CDE。
(3)设在Rt△BCD中,BC边上的高为h,
∵CD=1,∠BCD=60°,BD⊥CD
∴
∴
∴
即点C到平面DEF的距离为
∴ 。
。
∴ED⊥AD
又平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,
∴ED⊥平面ABCD
∴ED⊥BD
又BD⊥CD,且ED∩DC=D,
∴BD⊥平面CDE。
(2)∵G为DF的中点,且易知H是FC的中点,
则在△FCD中,GH∥CD
又∵CD
 平面CDE,GH
平面CDE,GH 平面CDE,
平面CDE, ∴GH∥平面CDE。
(3)设在Rt△BCD中,BC边上的高为h,
∵CD=1,∠BCD=60°,BD⊥CD
∴

∴

∴

即点C到平面DEF的距离为

∴
 。
。
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,在平行四边形ABCD中,下列结论中错误的是( )
如图,在平行四边形ABCD中,下列结论中错误的是( )A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
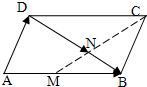 如图,在平行四边形ABCD,
如图,在平行四边形ABCD, 如图,在平行四边形ABCD中,
如图,在平行四边形ABCD中,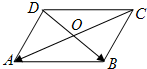 如图,在平行四边形ABCD中,若
如图,在平行四边形ABCD中,若 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的中点.