题目内容

15．曲线f（x）=2-xex在点（0，2）处的切线方程为x+y-2=0．

分析 求得函数的导数，求出切线的斜率，由斜截式方程可得所求切线的方程．

解答 解：f（x）=2-xex的导数为f′（x）=-（1+x）ex，
可得在点（0，2）处的切线斜率为k=-1，
即有在点（0，2）处的切线方程为y=-x+2，
即为x+y-2=0．
故答案为：x+y-2=0．

点评 本题考查导数的运用：求切线的方程，考查导数的几何意义：函数在某点处的导数即为曲线在该点处的导数，正确求导和运用直线方程是解题的关键．

练习册系列答案
相关题目
5．已知f（x）=Asin（2x+φ），其中A＞0．
（1）若?x∈R，使f（x+a）-f（x）=2A成立，则实数a的最小值是$\frac{π}{2}$；
（2）若A=1，则f（x+$\frac{π}{6}$）-f（x）的最大值为1．
6．已知l，m，n是不同的直线，α，β，γ是不重合的平面，下列命题中正确的个数为（　　）
①若m⊥α，m⊥β，则α∥β；②若α⊥γ，β⊥γ，则α∥β
③若m∥α，m∥β，则α∥β；④l∥α，m?α，则l∥m．
A．1B．2C．3D．4
3．已知集合A={0，a-2，3}，若{-2，0}⊆A，则实数a的值为（　　）
A．0B．1C．2D．3
10．设角A，B，C是△ABC的三个内角，则“A+B＜C”是“△ABC是钝角三角形”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
20．已知数列{an}的各项均不为零，其前n项和为Sn，Sn=2an-2（n∈N*），设${b_n}=\frac{3^n}{{{2^n}{S_n}}}$，数列{bn}的前n项和为Tn．
（Ⅰ）比较bn+1与$\frac{3}{4}{b_n}$的大小（n∈N*）；
（Ⅱ）证明：（2n-1）bn≤T2n-1＜3，n∈N*．
7．已知i是虚数单位，则复数$\frac{5+3i}{4-i}$的共轭复数是（　　）
A．1-iB．-1+iC．1+iD．-1-i
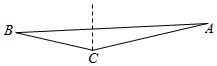4．若实数x满足x2-3x+2＜0，则$\frac{ln{x}^{2}}{{x}^{2}}$，（$\frac{lnx}{x}$）2，$\frac{lnx}{x}$三者的大小关系是x∈$（1，\sqrt{e}）$时，$（\frac{lnx}{x}）^{2}$＜$\frac{lnx}{x}$$＜\frac{ln{x}^{2}}{{x}^{2}}$；
$\sqrt{e}$＜x＜2时，$\frac{lnx}{x}$＞$\frac{ln{x}^{2}}{{x}^{2}}$＞$（\frac{lnx}{x}）^{2}$．．
5．如图，一艘船现在灯塔C北偏东75°的点A且AC=3海里，当船航行了$\sqrt{21}$海里后到达点B，若点B在灯塔C西偏北15°方向上，则B，C两点的距离为$\sqrt{3}$海里．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网