题目内容
13.已知数列{an}的各项均为正数,Sn为其前n项和,且对任意的n∈N*,均有an,Sn,$a_n^2$成等差数列,则an=n.分析 由已知条件推导出2an=an+an2-an-1-an-12,从而得到{an}是公差为1的等差数列,由此能求出an=n.
解答 解:∵各项均为正数的数列{an}的前n项和为Sn,
对任意n∈N*,总有an,Sn,an2成等差数列,
∴2Sn=an+an2,2Sn-1=an-1+an-12,
两式相减,得2an=an+an2-an-1-an-12,
∴an+an-1=(an+an-1)(an-an-1),
又an,an-1为正数,∴an-an-1=1,n≥2,
∴{an}是公差为1的等差数列,
当n=1时,2S1=a1+a12,得a1=1,或a1=0(舍),
∴an=n.
故答案为:n.
点评 本题考查数列的通项公式的求法,解题时要认真审题,属于中档题.

练习册系列答案
相关题目
4.若等式x4+4x3+3x2+2x+1=(x+1)4+a(x+1)3+b(x+1)2+c(x+1)+d恒成立,则(a,b,c,d)等于( )
| A. | (1,2,3,-1) | B. | (2,3,4,-1) | C. | (0,-1,2,-2) | D. | (0,-3,4,-1) |
1.执行右面的程序框图,如果输入的N=3,那么输出的S=( )
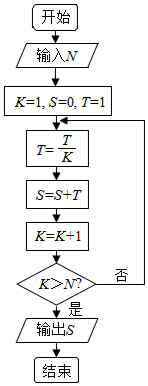

| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{5}{3}$ | D. | $\frac{5}{2}$ |
18.已知x,y满足约束条件$\left\{\begin{array}{l}{x≥0}\\{x+y≥2}\\{2x+y≤4}\end{array}\right.$,则(x+1)2+y2的最小值为( )
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{9}{2}$ | D. | 5 |
5.平面向量$\overrightarrow{a}$=(1,x),$\overrightarrow{b}$=(-2,3),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数x的值为( )
| A. | -6 | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | 0 |